题目内容
已知tanα=3,π<α<
,
(1)求cosα的值
(2)求sin(
+α)+sin(π+α)的值.
| 3π |
| 2 |
(1)求cosα的值
(2)求sin(
| π |
| 2 |
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:(1)由tanα的值及α的范围,利用同角三角函数间的基本关系求出cosα的值即可;
(2)由cosα的值及α的范围,利用同角三角函数间的基本关系求出sinα的值,原式利用诱导公式变形后将各自的值代入计算即可求出值.
(2)由cosα的值及α的范围,利用同角三角函数间的基本关系求出sinα的值,原式利用诱导公式变形后将各自的值代入计算即可求出值.
解答:
解:(1)∵tanα=3,π<α<
,
∴cosα=-
=-
;
(2)∵cosα=-
,π<α<
,
∴sinα=-
=-
,
则原式=cosα-sinα=
.
| 3π |
| 2 |
∴cosα=-
|
| ||
| 10 |
(2)∵cosα=-
| ||
| 10 |
| 3π |
| 2 |
∴sinα=-
| 1-cos2α |
3
| ||
| 10 |
则原式=cosα-sinα=
| ||
| 5 |
点评:此题考查了同角三角函数基本关系的运用,以及诱导公式的作用,熟练掌握基本关系是解本题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
i是虚数单位,则(1+i)(2+i)=( )
| A、1+3i | B、4+3i |
| C、3+3i | D、1 |
在二项式(x-
)n的展开式中恰好第5项的二项式系数最大,则展开式中含x2项的系数是( )
| 1 |
| x |
| A、-56 | B、-35 |
| C、35 | D、56 |
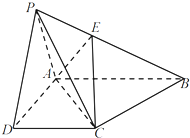 如图,四棱锥P-ABCD的底面是直角梯形,其中AB⊥AD,DC⊥AD,AB=AD=2,DC=1.侧面正△PAD所在平面与底面垂直.
如图,四棱锥P-ABCD的底面是直角梯形,其中AB⊥AD,DC⊥AD,AB=AD=2,DC=1.侧面正△PAD所在平面与底面垂直.