题目内容
设A,B是椭圆W:
+
=1上不关于坐标轴对称的两个点,直线AB交x轴于点M(与点A,B不重合),O为坐标原点.
(Ⅰ)如果点M是椭圆W的右焦点,线段MB的中点在y轴上,求直线AB的方程;
(Ⅱ)设N为x轴上一点,且
•
=4,直线AN与椭圆W的另外一个交点为C,证明:点B与点C关x轴对称.
| x2 |
| 4 |
| y2 |
| 3 |
(Ⅰ)如果点M是椭圆W的右焦点,线段MB的中点在y轴上,求直线AB的方程;
(Ⅱ)设N为x轴上一点,且
| OM |
| ON |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由已知条件推导出点B的坐标为(-1,±
),由此能求出直线AB(即MB)的方程.
(Ⅱ)设点B关于x轴的对称点为B1(在椭圆W上),要证点B与点C关于x轴对称,只要证点B1与点C重合,又因为直线AN与椭圆W的交点为C(与点A不重合),所以只要证明点A,N,B1三点共线.
| 3 |
| 2 |
(Ⅱ)设点B关于x轴的对称点为B1(在椭圆W上),要证点B与点C关于x轴对称,只要证点B1与点C重合,又因为直线AN与椭圆W的交点为C(与点A不重合),所以只要证明点A,N,B1三点共线.
解答:
(Ⅰ)解:椭圆W:
+
=1的右焦点为M(1,0),
因为线段MB的中点在y轴上,
所以点B的横坐标为-1,
因为点B在椭圆W上,
将x=-1代入椭圆W的方程,得点B的坐标为(-1,±
).
所以直线AB(即MB)的方程为3x-4y-3=0或3x+4y-3=0.
(Ⅱ)证明:设点B关于x轴的对称点为B1(在椭圆W上),
要证点B与点C关于x轴对称,
只要证点B1与点C重合,.
又因为直线AN与椭圆W的交点为C(与点A不重合),
所以只要证明点A,N,B1三点共线.
以下给出证明:
由题意,设直线AB的方程为y=kx+m,(k≠0),A(x1,y1),B(x2,y2),则B1(x2,-y2).
由
,
得(3+4k2)x2+8kmx+4m2-12=0,
所以△=(8km)2-4(3+4k2)(4m2-12)>0,
x1+x2=-
,x1x2=
.
在y=kx+m中,令y=0,得点M的坐标为(-
,0),
由
•
=4,得点N的坐标为N(-
,0),
设直线NA,NB1的斜率分别为kNA,kNB1,
则kNA-kNB1=
-
=
,
因为x2y1+y1×
+x1y2+y2×
=x2(kx1+m)+(kx1+m)×
+x1(kx2+m)+(kx2+m)×
=2kx1x2+(m+
)(x1+x2)+8k
=2k×(
)+(m+
)(-
)+8k
=
=0.
所以kNA-kNB1=0,
所以点A,N,B1三点共线,
即点B与点C关于x轴对称.
| x2 |
| 4 |
| y2 |
| 3 |
因为线段MB的中点在y轴上,
所以点B的横坐标为-1,
因为点B在椭圆W上,
将x=-1代入椭圆W的方程,得点B的坐标为(-1,±
| 3 |
| 2 |
所以直线AB(即MB)的方程为3x-4y-3=0或3x+4y-3=0.
(Ⅱ)证明:设点B关于x轴的对称点为B1(在椭圆W上),
要证点B与点C关于x轴对称,
只要证点B1与点C重合,.
又因为直线AN与椭圆W的交点为C(与点A不重合),
所以只要证明点A,N,B1三点共线.
以下给出证明:
由题意,设直线AB的方程为y=kx+m,(k≠0),A(x1,y1),B(x2,y2),则B1(x2,-y2).
由
|
得(3+4k2)x2+8kmx+4m2-12=0,
所以△=(8km)2-4(3+4k2)(4m2-12)>0,
x1+x2=-
| 8km |
| 3+4k2 |
| 4m2-12 |
| 3+4k2 |
在y=kx+m中,令y=0,得点M的坐标为(-
| m |
| k |
由
| OM |
| ON |
| 4k |
| m |
设直线NA,NB1的斜率分别为kNA,kNB1,
则kNA-kNB1=
| y1 | ||
x1+
|
| -y2 | ||
x2+
|
=
x2y1+y1×
| ||||
(x1+
|
因为x2y1+y1×
| 4k |
| m |
| 4k |
| m |
=x2(kx1+m)+(kx1+m)×
| 4k |
| m |
| 4k |
| m |
=2kx1x2+(m+
| 4k2 |
| m |
=2k×(
| 4m2-12 |
| 3+4k2 |
| 4k2 |
| m |
| 8km |
| 3+4k2 |
=
| 8m2k-24k-8m2k-32k3+24k+32k3 |
| 3+4k2 |
=0.
所以kNA-kNB1=0,
所以点A,N,B1三点共线,
即点B与点C关于x轴对称.
点评:本题考查直线方程的求法,考查两点关于x轴对称的证明,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
不等式组
在坐标平面内表示的图形的面积等于( )
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
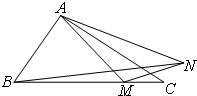 如图,已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°,
如图,已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°,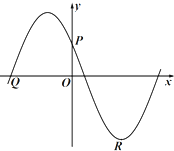 如图,点P(0,
如图,点P(0,