题目内容
已知二次函数f(x)的最大值为2,且f(1)=f(3)=0.
(1)求f(x)的解析式;
(2)若函数f(x)在区间[m,m+1]上单调,求实数m的取值范围.
(1)求f(x)的解析式;
(2)若函数f(x)在区间[m,m+1]上单调,求实数m的取值范围.
考点:二次函数在闭区间上的最值,二次函数的性质
专题:综合题
分析:求二次函数的解析式常用待定系数法,由于已知f(1)=f(3)=0,因此设两根式比较好;二次函数在某一区间上单调,只需要二次函数的对称轴在区间左侧或右侧.
解答:
解:(1)∵f(1)=f(3)=0,∴设f(x)=a(x-1)(x-3),函数f(x)的对称轴为x=2,
函数f(x)在x=2上取得最大值2,
∴f(2)=-a=2,解得a=-2,
所以函数的解析式为f(x)=-2x2+8x-6;
(2)要使函数f(x)在区间[m,m+1]上单调,则需m≥2或m+1≤2,即m≥2或m≤1,
故当函数f(x)在区间[m,m+1]上单调时,m的取值范围为(-∞,1]或[2,+∞).
函数f(x)在x=2上取得最大值2,
∴f(2)=-a=2,解得a=-2,
所以函数的解析式为f(x)=-2x2+8x-6;
(2)要使函数f(x)在区间[m,m+1]上单调,则需m≥2或m+1≤2,即m≥2或m≤1,
故当函数f(x)在区间[m,m+1]上单调时,m的取值范围为(-∞,1]或[2,+∞).
点评:本题考查了用待定系法求二次函数解析式的方法,关键是选择适当的形式;研究二次函数的单调性主要是研究对称轴与区间的关系.

练习册系列答案
相关题目
已知集合A={x|x2-6x+5≤0}和B={y|y=2x+2},则A∩B( )
| A、ϕ | B、[1,2) |
| C、[1,5] | D、(2,5] |
 已知抛物线C:x2=2py(p>0)上一个纵坐标为2的点到焦点F的距离为3.
已知抛物线C:x2=2py(p>0)上一个纵坐标为2的点到焦点F的距离为3. 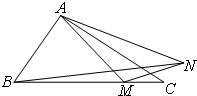 如图,已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°,
如图,已知△ABC中,AB=1,AC=2,∠BAC=120°,点M是边BC上的动点,动点N满足∠MAN=30°, 如图,点P(0,
如图,点P(0,