题目内容
14.若loga3b=-1,则a+b的最小值为$\frac{2\sqrt{3}}{3}$.分析 把对数式化为指数式,再利用基本不等式的性质即可得出.
解答 解:∵loga3b=-1,∴a-1=3b,解得ab=$\frac{1}{3}$.a,b>0.
则a+b≥2$\sqrt{ab}$=$\frac{2\sqrt{3}}{3}$,当且仅当a=b=$\frac{\sqrt{3}}{3}$时取等号,其最小值为$\frac{2\sqrt{3}}{3}$.
故答案为:$\frac{2\sqrt{3}}{3}$.
点评 本题考查了对数式化为指数式、基本不等式的性质,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.下列比较大小错误的是( )
| A. | sin($-\frac{π}{18}$)>sin($-\frac{π}{10}$) | B. | sin250°>sin260° | C. | tan$\frac{π}{4}$>tan$\frac{π}{6}$ | D. | tan138°>tan143° |
4.点M的极坐标(1,π)化成直角坐标为( )
| A. | (1,0) | B. | (-1,0) | C. | (0,1) | D. | (0,-1) |
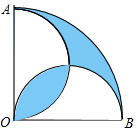 如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆,设OA=1,则阴影部分的面积是$\frac{π-2}{4}$.
如图,在圆心角为直角的扇形OAB中,分别以OA,OB为直径作两个半圆,设OA=1,则阴影部分的面积是$\frac{π-2}{4}$.