题目内容
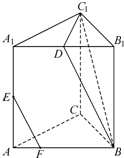 如图,三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=
如图,三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=| 1 |
| 4 |
(Ⅰ)求证:EF∥平面BDC1;
(Ⅱ)在棱AC上是否存在一个点G,使得平面EFG将三棱柱分割成的两部分体积之比为1:31,若存在,指出点G的位置;若不存在,请说明理由.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定
专题:综合题,空间位置关系与距离
分析:(I)取AB的中点M,根据AF=
AB,得到F为AM的中点,又E为AA1的中点,根据三角形中位线定理得EF∥A1M,从而在三棱柱ABC-A1B1C1中,A1DBM为平行四边形,进一步得出EF∥BD.最后根据线面平行的判定即可证出EF∥平面BC1D.
(II)对于存在性问题,可先假设存在,即假设在棱AC上存在一个点G,使得平面EFG将三棱柱分割成的两部分体积之比为1:31,再利用棱柱、棱锥的体积公式,求出AG与AC的比值,若出现矛盾,则说明假设不成立,即不存在;否则存在.
| 1 |
| 4 |
(II)对于存在性问题,可先假设存在,即假设在棱AC上存在一个点G,使得平面EFG将三棱柱分割成的两部分体积之比为1:31,再利用棱柱、棱锥的体积公式,求出AG与AC的比值,若出现矛盾,则说明假设不成立,即不存在;否则存在.
解答:
 (I)证明:取AB的中点M,
(I)证明:取AB的中点M,
∵AF=
AB,∴F为AM的中点,
又∵E为AA1的中点,∴EF∥A1M
在三棱柱ABC-A1B1C1中,D,M分别为A1B1,AB的中点,
∴A1D∥BM,A1D=BM,
∴A1DBM为平行四边形,∴AM∥BD
∴EF∥BD.
∵BD?平面BC1D,EF?平面BC1D,
∴EF∥平面BC1D.
(II)解:设AC上存在一点G,使得平面EFG将三棱柱分割成两部分的体积之比为1:31,
则VE-AFG:VABC-A1B1C1=1:32,
∴(
×
AF•AGsin∠GAF•AE):
AB•ACsin∠CAB•AA1=
•
∴
•
=
,∴
=
,
∴AG=
AC.
∴符合要求的点G存在.
 (I)证明:取AB的中点M,
(I)证明:取AB的中点M,∵AF=
| 1 |
| 4 |
又∵E为AA1的中点,∴EF∥A1M
在三棱柱ABC-A1B1C1中,D,M分别为A1B1,AB的中点,
∴A1D∥BM,A1D=BM,
∴A1DBM为平行四边形,∴AM∥BD
∴EF∥BD.
∵BD?平面BC1D,EF?平面BC1D,
∴EF∥平面BC1D.
(II)解:设AC上存在一点G,使得平面EFG将三棱柱分割成两部分的体积之比为1:31,
则VE-AFG:VABC-A1B1C1=1:32,
∴(
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 24 |
| AG |
| AC |
∴
| 1 |
| 24 |
| AG |
| AC |
| 1 |
| 32 |
| AG |
| AC |
| 3 |
| 4 |
∴AG=
| 3 |
| 4 |
∴符合要求的点G存在.
点评:本题考查线面平行,考查棱柱、棱锥、棱台的体积的计算,解题的关键是利用线面平行的判定证明线面平行,属于中档题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目