题目内容
已知:直线l:x+2y-1=0与⊙C:x2+y2-2x-4y+m=0(m<5)
(1)若直线l与⊙C相交,求m的取值范围.
(2)在(1)的条件下,设直线l与⊙C交于A、B两点,若OA⊥OB,求m的值.
(1)若直线l与⊙C相交,求m的取值范围.
(2)在(1)的条件下,设直线l与⊙C交于A、B两点,若OA⊥OB,求m的值.
考点:直线与圆的位置关系
专题:直线与圆
分析:(1)先求出圆心和半径,根据圆心到直线的距离小于半径,可得
<
,由此求得m的取值范围.
(2)把直线方程和圆的方程联立方程组化简,利用韦达定理、两个向量垂直的性质,求出m的值.
| |1+4-1| | ||
|
| 5-m |
(2)把直线方程和圆的方程联立方程组化简,利用韦达定理、两个向量垂直的性质,求出m的值.
解答:
解:(1)⊙C:x2+y2-2x-4y+m=0 即 (x-1)2+(y-2)2=5-m,
表示以C(1,2)为圆心、半径等于
的圆.
根据圆心到直线l:x+2y-1=0的距离为d=
=
<
,
解得 m<
,故m的取值范围(-∞,
).
(2)由
可得 5y2-4y+m-1=0,∴y1+y2=
,y1•y2=
.
再根据OA⊥OB,可得
•
=x1•x2+y1•y2=(1-2y1)(1-2y2)+y1•y2=1+5y1•y2-2(y1+y2)
=1+5•
-2×
=0,
解得 m=
.
表示以C(1,2)为圆心、半径等于
| 5-m |
根据圆心到直线l:x+2y-1=0的距离为d=
| |1+4-1| | ||
|
4
| ||
| 5 |
| 5-m |
解得 m<
| 9 |
| 5 |
| 9 |
| 5 |
(2)由
|
| 4 |
| 5 |
| m-1 |
| 5 |
再根据OA⊥OB,可得
| OA |
| OB |
=1+5•
| m-1 |
| 5 |
| 4 |
| 5 |
解得 m=
| 8 |
| 5 |
点评:本题主要考查直线和圆的位置关系,点到直线的距离公式的应用.还考查了韦达定理、两个向量垂直的性质,属于基础题.

练习册系列答案
相关题目
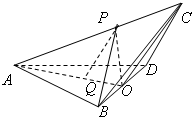 如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且
如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且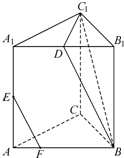 如图,三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=
如图,三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=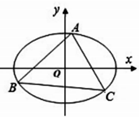 已知椭圆C:
已知椭圆C: