题目内容
在△ABC中,内角A,B,C所对的边分别是a,b,c,已知a=2,c=
,且sinC=
sinB.
(Ⅰ)求b的值;
(Ⅱ)求△ABC的面积.
| 2 |
| 2 |
(Ⅰ)求b的值;
(Ⅱ)求△ABC的面积.
考点:正弦定理,余弦定理
专题:解三角形
分析:(Ⅰ)由正弦定理和已知等式求得b和c的关系,求得b.
(Ⅱ)由余弦定理求得cosC的值,继而求得sinC的值,最后利用三角形面积公式求得答案.
(Ⅱ)由余弦定理求得cosC的值,继而求得sinC的值,最后利用三角形面积公式求得答案.
解答:
解:(Ⅰ)∵sinC=
sinB,
∴c=
b,
∴b=
c=1.
(Ⅱ)由余弦定理知cosC=
=
,
∴sinC=
=
,
∴S=
absinC=
×2×1×
=
.
| 2 |
∴c=
| 2 |
∴b=
| ||
| 2 |
(Ⅱ)由余弦定理知cosC=
| a2+b2-c2 |
| 2ab |
| 3 |
| 4 |
∴sinC=
| 1-cos2C |
| ||
| 4 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |
点评:本题主要考查了正弦定理和余弦定理的应用.第一问解题的关键是运用正弦定理完成边角问题的转化.

练习册系列答案
相关题目
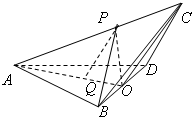 如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且
如图,三棱锥C-ABD中,AB=AD=BD=BC=CD=2,O为BD的中点,∠AOC=120°,P为AC上一点,Q为AO上一点,且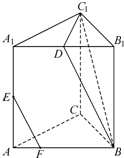 如图,三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=
如图,三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=