题目内容

已知cos（π+α）=
4
5
，α为第三象限角．
（1）求sinα，tanα的值；
（2）求sin（α+
π
4
），tan2α的值．
考点：同角三角函数基本关系的运用
专题：三角函数的求值
分析：（1）依题意，利用同角三角函数基本关系可求得sinα，tanα的值；
（2）利用两角和的正弦与正切即可sin（α+
π
4
），tan2α的值．
解答： 解：（1）由条件得cosα=-
4
5
，α为第三象限角，
∴sinα=-
1-cos2α
=-
1-(-
4
5
)2
=-
3
5
；…（2分）
∴tanα=
sinα
cosα
=
-
3
5
-
4
5
=
3
4
；           …（4分）
（2）由（1）得sin（α+
π
4
）=sinαcos
π
4
+cosαsin
π
4
=（-
3
5
）×
2
2
+（-
4
5
）×
2
2
=-
7
2
10
，…（6分）
tan2α=
2tanα
1-tan2α
=
2×
3
4
1-(-
3
4
)2
=
24
7
…（8分）
点评：本题考查同角三角函数基本关系的运用，考查两角和的正弦与正切，考查运算求解能力，属于中档题．
练习册系列答案
相关题目
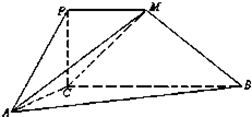如图，四边形PCBM是直角梯形，∠PCB=90°，PM∥BC，PM=1，BC=2．又AC=1，∠ACB=120°，AB⊥PC，直线AM与直线PC所成的角为60°．
（Ⅰ）求证：PC⊥AC；
（Ⅱ）求三棱锥VB-MAC的体积．
已知sinα=
4
7
3
，sin（α+β）=
5
14
3
，α∈（0，
π
2
），α+β∈（
π
2
，π），求β的值．
已知函数f（x）对任意实数x，y都有f（xy）=f（x）+f（y）成立．
（1）求f（0）和f（1）的值．
（2）若f（2）=a，f（3）=b（a，b均为常数），求f（36）的值．
已知函数f（x）=sin（x+
π
12
）．
（1）求f（-
π
4
）的值；
（2）若cosθ=
4
5
，θ∈（0，
π
2
），求f（2θ-
π
3
）．
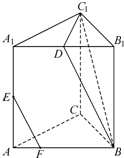如图，三棱柱ABC-A1B1C1中，∠BAC=90°，AA1⊥平面ABC，D、E分别为A1B1、AA1的中点，点F在棱AB上，且AF=
1
4
AB．
（Ⅰ）求证：EF∥平面BDC1；
（Ⅱ）在棱AC上是否存在一个点G，使得平面EFG将三棱柱分割成的两部分体积之比为1：31，若存在，指出点G的位置；若不存在，请说明理由．
已知方程x2+y2-2x+2my+m2-2m-2=0（m∈R）．
（1）若方程表示圆，求实数m的取值范围；
（2）若方程表示的圆C的圆心C（1，1），求经过P（2，4）的圆C的切线方程；
（3）若直线x+y+t=0与（2）中的圆C交于A、B两点，且△ABC是直角三角形，求实数t的值．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率是
2
2
，且点P（1，
2
2
）在椭圆上．
（1）求椭圆的方程；
（2）若过点D（0，2）的直线l与椭圆C交于不同的两点E，F，试求△OEF面积的取值范围（O为坐标原点）．
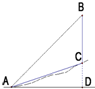如图，在坡角为15°（∠CAD=15°）的山坡顶上有一个高度为50米的中国移动信号塔BC，在坡底A处测得塔顶B的仰角为45°（∠BAD=45°），则塔顶到水平面AD的距离（BD）约为
 
米．（结果保留整数，
3
≈1.732）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网