题目内容
已知Ω={(x,y)|0≤x≤1,0≤y≤1},A是曲线(x-1)2+y2=1与y=x围成的区域,若向区域Ω内随机投一点P,则点P落入区域A的概率为 .
考点:几何概型
专题:概率与统计
分析:作出区域对应的图象,求出对应的面积,利用几何概型的概率公式即可得到结论.
解答:
解:Ω={(x,y)|0≤x≤1,0≤y≤1}对应的区域为矩形,面积S=1×1=1,
区域A对应的区域为阴影部分,对应的面积S=
π×12-
×1×1=
-
,
则若向区域Ω内随机投一点P,则点P落入区域A的概率P=
=
 ,
,
故答案为:
区域A对应的区域为阴影部分,对应的面积S=
| 1 |
| 4 |
| 1 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
则若向区域Ω内随机投一点P,则点P落入区域A的概率P=
| ||||
| 1 |
| π-2 |
| 4 |
 ,
,故答案为:
| π-2 |
| 4 |
点评:本题主要考查几何概型的概率计算,求出对应区域的面积是解决本题的关键.

练习册系列答案
相关题目
设x∈R,则“x2>4”是“x>2”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
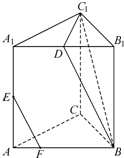 如图,三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=
如图,三棱柱ABC-A1B1C1中,∠BAC=90°,AA1⊥平面ABC,D、E分别为A1B1、AA1的中点,点F在棱AB上,且AF=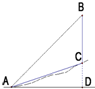 如图,在坡角为15°(∠CAD=15°)的山坡顶上有一个高度为50米的中国移动信号塔BC,在坡底A处测得塔顶B的仰角为45°(∠BAD=45°),则塔顶到水平面AD的距离(BD)约为
如图,在坡角为15°(∠CAD=15°)的山坡顶上有一个高度为50米的中国移动信号塔BC,在坡底A处测得塔顶B的仰角为45°(∠BAD=45°),则塔顶到水平面AD的距离(BD)约为