题目内容
已知直线l1：2x-3y+1=0，l2：x+y-2=0的交点为P．
（1）求点P的坐标；
（2）求过点P且与直线l2垂直的直线l的方程．
（1）求点P的坐标；
（2）求过点P且与直线l2垂直的直线l的方程．
考点：直线的一般式方程与直线的垂直关系
专题：直线与圆
分析：（1）由
，能求出点P的坐标．
（2）直线l2的斜率为-1，由l2⊥l，知直线l的斜率为1，由此利用点斜式方程能求出l的方程．
|
（2）直线l2的斜率为-1，由l2⊥l，知直线l的斜率为1，由此利用点斜式方程能求出l的方程．
解答：
解：（1）由
，得
，…（5分）
点P的坐标为（1，1）．
（2）直线l2的斜率为-1，…（7分）
而l2⊥l，则直线l的斜率为1，…（9分）
由点斜式可得l的方程为y-1=x-1，即x-y=0．…（12分）
|
|
点P的坐标为（1，1）．
（2）直线l2的斜率为-1，…（7分）
而l2⊥l，则直线l的斜率为1，…（9分）
由点斜式可得l的方程为y-1=x-1，即x-y=0．…（12分）
点评：本题考查点的坐标的求法，考查直线方程的求法，注意直线位置关系的合理运用．
练习册系列答案
相关题目
在等比数列{an}中，如果a1=2，公比q=2，则a4的值为（ ）
| A、4 | B、16 | C、8 | D、32 |
∫
（cos
x+
）dx的值为（ ）
2 0 |
| π |
| 2 |
| 4-x2 |
| A、2π | ||
| B、π | ||
| C、π+1 | ||
D、π+
|
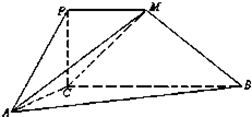如图，四边形PCBM是直角梯形，∠PCB=90°，PM∥BC，PM=1，BC=2．又AC=1，∠ACB=120°，AB⊥PC，直线AM与直线PC所成的角为60°．
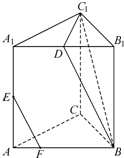如图，三棱柱ABC-A1B1C1中，∠BAC=90°，AA1⊥平面ABC，D、E分别为A1B1、AA1的中点，点F在棱AB上，且AF=