题目内容
已知双曲线C的左右焦点为F1,F2,其中一条渐近线为y=
x,点A在双曲线C上,若|F1A|=2|F2A|,则cos∠AF2F1=( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:计算题,解三角形,直线与圆,圆锥曲线的定义、性质与方程
分析:由已知得渐近线的斜率为
,即有b=
a,再求c=2a,运用双曲线的定义和条件,求得三角形AF2F1的三边,再由余弦定理,即可得到所求值.
| 3 |
| 3 |
解答:
解:由于双曲线的一条渐近线y=
x,且为y=
x,则斜率为
,
即有b=
a,c=
=2a,
|F1A|=2|F2A|,且由双曲线的定义,可得|F1A|-|F2A|=2a,
解得,|F1A|=4a,|F2A|=2a,
又|F1F2|=2c,由余弦定理,可得
cos∠AF2F1=
=
=
.
故选A.
| b |
| a |
| 3 |
| 3 |
即有b=
| 3 |
| a2+b2 |
|F1A|=2|F2A|,且由双曲线的定义,可得|F1A|-|F2A|=2a,
解得,|F1A|=4a,|F2A|=2a,
又|F1F2|=2c,由余弦定理,可得
cos∠AF2F1=
| |AF2|2+|F1F2|2-|AF1|2 |
| 2|AF2|•|F1F2| |
| 4a2+4×4a2-16a2 |
| 2×2a×4a |
| 1 |
| 4 |
故选A.
点评:本题考查双曲线的定义和性质,考查余弦定理的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
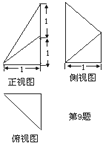
一个几何体的三视图如图所示,则它的体积为( )

A、
| ||||
B、
| ||||
C、
| ||||
D、
|
与向量
=(1,2,3),
=(3,1,2)都垂直的向量为( )
| a |
| b |
| A、(1,7,5) |
| B、(1,-7,5) |
| C、(-1,-7,5) |
| D、(1,-7,-5) |