题目内容
与向量
=(1,2,3),
=(3,1,2)都垂直的向量为( )
| a |
| b |
| A、(1,7,5) |
| B、(1,-7,5) |
| C、(-1,-7,5) |
| D、(1,-7,-5) |
考点:向量的数量积判断向量的共线与垂直
专题:空间向量及应用
分析:直接利用空间向量的数量积为0,判断空间向量垂直,得到选项即可.
解答:
解:由题意可知:(-1,-7,5)•(1,2,3)=0,
(3,1,2)•(-1,-7,5)=0.
所以与向量
=(1,2,3),
=(3,1,2)都垂直的向量为(-1,-7,5).
故选:C.
(3,1,2)•(-1,-7,5)=0.
所以与向量
| a |
| b |
故选:C.
点评:本题考查空间向量的数量积的应用,空间向量的垂直体积的应用,考查计算能力.

练习册系列答案
相关题目
已知双曲线C的左右焦点为F1,F2,其中一条渐近线为y=
x,点A在双曲线C上,若|F1A|=2|F2A|,则cos∠AF2F1=( )
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设θ为两个非零向量
,
的夹角,已知对任意实数t,|
-t
|的最小值是2,则( )
| a |
| b |
| b |
| a |
A、若θ确定,则|
| ||
B、若θ确定,则|
| ||
C、若|
| ||
D、若|
|
已知方程x2+xlog26+log23=0的两根为α,β,则(
)α•(
)β=( )
| 1 |
| 4 |
| 1 |
| 4 |
A、
| ||
| B、36 | ||
| C、-6 | ||
| D、6 |
执行如图所示的程序框图,输出的T=( )


| A、29 | B、44 | C、52 | D、62 |
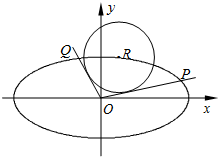 如图,在平面直角坐标系xOy中,已知椭圆C:
如图,在平面直角坐标系xOy中,已知椭圆C: