Question

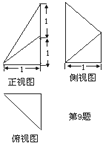
一个几何体的三视图如图所示，则它的体积为（　　）

• A、

  3

  2

• B、

  1

  2

• C、

  3

  2

• D、

  3

  2

  +1

Answer 1

考点：由三视图求面积、体积

专题：计算题,空间位置关系与距离

分析：三视图中长对正，高对齐，宽相等；由三视图想象出直观图，一般需从俯视图构建直观图，该几何体为四棱锥．

解答： 解：该几何体为四棱锥．
其底面为梯形，
上底为1，下底为2，高为1；
体高为1；
故V=

1

3

×

1

2

×（1+2）×1×1=

1

2

；
故选B．

点评：三视图中长对正，高对齐，宽相等；由三视图想象出直观图，一般需从俯视图构建直观图，本题考查了学生的空间想象力，识图能力及计算能力．