题目内容
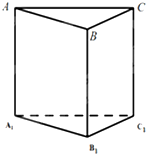 如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2
如图,已知三棱柱ABC-A1B1C1的六个顶点都在球O的球面上,若AA1⊥平面A1B1C1,A1B1⊥B1C1,AA1=8,A1B1=6,A1C1=2| 34 |
A、
| ||||
B、
| ||||
C、360
| ||||
D、
|
考点:球内接多面体,球的体积和表面积
专题:计算题,空间位置关系与距离
分析:通过球的内接体,将三棱柱ABC-A1B1C1还原成长方体,球的直径是其对角线的长,求出球的半径,即可求出球O的体积.
解答:
解:由题意,三棱柱的底面是直角三角形,侧棱与底面垂直,将三棱柱ABC-A1B1C1还原成长方体,球的直径是其对角线的长,
因为AA1=8,A1B1=6,A1C1=2
,所以球的直径是
=10
所以球的半径为:5
,
所以球O的体积为
×(5
)3=
π.
故选D.
因为AA1=8,A1B1=6,A1C1=2
| 34 |
| 4×34+64 |
| 2 |
所以球的半径为:5
| 2 |
所以球O的体积为
| 4π |
| 3 |
| 2 |
1000
| ||
| 3 |
故选D.
点评:本题考查球的内接体与球的关系,球的半径的求解,考查球O的体积,考查计算能力,确定球的半径是关键.

练习册系列答案
相关题目
在长为6cm的线段AB上任取一点C,现作一矩形,邻边长分别等于线段AC,BC的长,则该矩形面积小于8cm2,的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
设双曲线
-
=1(a>0,b>0)的离心率为
,且它的一个焦点与抛物线y2=24x的焦点重合,则此双曲线的方程为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
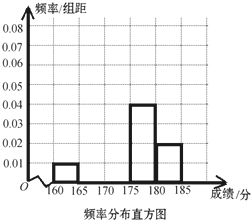 永安市教育局在2013年高职单招考试成绩中随机抽取100名学生的成绩,按成绩分组,得到频率分布表如下所示:
永安市教育局在2013年高职单招考试成绩中随机抽取100名学生的成绩,按成绩分组,得到频率分布表如下所示: