题目内容
1.如图,在矩形ABCD中,M是BC的中点,N是CD的中点,若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则λμ=$\frac{12}{25}$.
分析 以A为坐标原点建立坐标系,设矩形的长宽分别为2a,2b,得到A,B,C,M,N的坐标,利用向量相等得到关于λ,μ的方程组解之.
解答 解:以A为坐标原点建立坐标系,设矩形的长宽分别为2a,2b,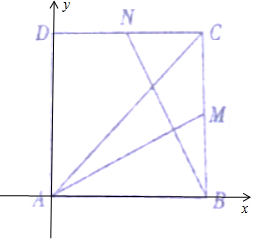
得到A(0,0),B(2a,0),C(2a,2b),
M(2a,b),N(a,2b),
所以$\overrightarrow{AC}$=(2a,2b),$\overrightarrow{AM}$=(2a,b),$\overrightarrow{BN}$=(-a,2b),
由$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$,则$\left\{\begin{array}{l}{2a=2aλ-aμ}\\{2b=bλ+2bμ}\end{array}\right.$,解得$\left\{\begin{array}{l}{λ=\frac{6}{5}}\\{μ=\frac{2}{5}}\end{array}\right.$,
所以λμ=$\frac{12}{25}$;
故答案为:$\frac{12}{25}$
点评 本题考查了平面向量基本定理的运用,利用坐标法使得计算简便,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
12.已知随机事件A与B,经计算得到K2的范围是3.841<K2<6.635,则(如表是K2的临界值表,供参考)( )
| P(K2≥x0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| x0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 有95% 把握说事件A与B有关 | B. | 有95% 把握说事件A与B无关 | ||
| C. | 有99% 把握说事件A与B有关 | D. | 有99% 把握说事件A与B无关 |
9.设复数z满足|z-3-4i|=1,其中i为虚数单位,则|z|的最大值是( )
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
16.已知集合A={x|x2+2x-3≤0},B={x|0≤log4(x+2)≤1},则A∩B=( )
| A. | [-3,2] | B. | [-1,1] | C. | [-1,2] | D. | [1,2] |