题目内容
10.已知数列{an}为等差数列,且a3=5,a5=9,数列{bn}的前n项和Sn=$\frac{2}{3}$bn+$\frac{1}{3}$.(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)设cn=an|bn|,求数列{cn}的前n项的和Tn.
分析 (Ⅰ)根据等差数列的定义即可求出通项公式,再根据数列的递推公式即可求出{bn}的通项公式,
(Ⅱ)由错位相减求和法求出数列{cn}的前n项和Tn.
解答 解:(Ⅰ)数列{an}为等差数列,∴d=$\frac{1}{2}$(a5-a3)=2,
又∵a3=5,
∴a1=1,
∴an=2n-1,
当n=1时,S1=$\frac{2}{3}$b1+$\frac{1}{3}$,
∴b1=1,
当n≥2时,bn=Sn-Sn-1=$\frac{2}{3}$bn-$\frac{2}{3}$bn-1,
∴bn=-2bn-1,
即数列{bn}是首项为1,公比为-2的等比数列,
∴bn=(-2)n-1,
(Ⅱ)cn=an•|bn|=(2n-1)•2n-1,
∴Tn=1×1+3×21+5×22+…+(2n-3)•2n-2+(2n-1)2n-1,
则2Tn=1×2+3×22+5×23+…+(2n-3)•2n-1+(2n-1)2n,
相减,-Tn=1+2(22+23+…+•2n-1)-(2n-1)2n=1+2×$\frac{2-{2}^{n}}{1-2}$-(2n-1)2n=1+2n-1-4-(2n-1)2n=-3+(3-2n)2n,
∴Tn=(2n-3)•2n+3.
点评 本题考查数列的通项公式的求法和数列求和,解题时要注意公式的灵活运用,特别是错位相减求和法的合理运用.

练习册系列答案
相关题目
15.已知α是第二象限角,且$|{cos\frac{α}{3}}|=-cos\frac{α}{3}$,则$\frac{α}{3}$是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
2.如图,已知ABCD-A′B′C′D′为正方体,则下列结论错误的是( )
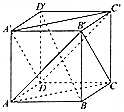

| A. | 平面ACB′∥平面A′C′D | B. | B′C⊥BD′ | ||
| C. | B′C⊥DC′ | D. | BD′⊥平面A′C′D |
19.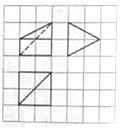 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥各个侧面中,最大的侧面面积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥各个侧面中,最大的侧面面积为( )
 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥各个侧面中,最大的侧面面积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某四棱锥的三视图,则该四棱锥各个侧面中,最大的侧面面积为( )| A. | 2 | B. | $\sqrt{5}$ | C. | 3 | D. | 4 |
