题目内容

9．设复数z满足|z-3-4i|=1，其中i为虚数单位，则|z|的最大值是（　　）
A．3B．4C．5D．6

分析 设z=x+yi，由复数z满足|z-3-4i）|=1可知，z在以（3，4）为圆心的单位圆上，由此求|z|的最大值．

解答 解：设z=x+yi，复数z满足|z-（3+4i）|=1，
所以（x-3）2+（y-4）2=1，表示（x，y）到点（3，4）的距离为1，所以（x，y）到原点的距离的最大值为$\sqrt{{3}^{2}+{4}^{2}}$+1=6；
故选：D．

点评 本题考查了复数的几何意义的运用；关键是明确已知z在以（3，4）为圆心的单位圆上．

练习册系列答案
相关题目
19．已知函数$f（x）=\left\{\begin{array}{l}-x+2，x≥a\\{x^2}+3x+2，x＜a.\end{array}\right.$恰有两个不同的零点，则a的取值范围是（1，+∞）．
20．（1）“已知函数f（x）=x2-mx+1对一切实数x，f（x）＞0恒成立”；
（2）“关于x的不等式x2＜9-m2有实数解”．
若以上结论中（1）错误并且（2）正确，则实数m的取值范围为（-3，-2]∪[2，3）．
17．已知曲线C的参数方程为$\left\{\begin{array}{l}{x=3cosθ}\\{y=2sinθ}\end{array}$（θ为参数），在同一平面直角坐标系中，将曲线C上的点按坐标变换$\left\{{\begin{array}{l}{x'=\frac{1}{3}x}\\{y'=\frac{1}{2}y}\end{array}}$得到曲线C'，以原点为极点，x轴的正半轴为极轴，建立极坐标系．
（1）写出曲线C与曲线C'的极坐标的方程； 
（2）若过点$A（{2\sqrt{2}，\frac{π}{4}}）$（极坐标）且倾斜角为$\frac{π}{3}$的直线l与曲线C交于M，N两点，弦MN的中点为P，求$\frac{|AP|}{|AM|•|AN|}$的值．
4．已知数列{an}，{bn}前n项和分别为Sn，Tn，an+1-an=2（bn+1-bn），b1=3，Sn=n2+2n+3，则Tn=$\frac{1}{2}$（n2+2n+3）．（n∈N*）．
14．已知直线l经过点P（-2，5），且斜率为$-\frac{3}{4}$，若直线m与l平行且两直线间的距离为3，则直线m的方程为3x+4y+1=0，或 3x+4y-29=0．
1．如图，在矩形ABCD中，M是BC的中点，N是CD的中点，若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$，则λμ=$\frac{12}{25}$．
18．已知一个直角三角形的两条直角边长分别是2，$2\sqrt{3}$；以这个直角三角形的斜边所在直线为旋转轴，其余两边旋转一周形成的面所围成的旋转体，求这个旋转体的表面积和体积．
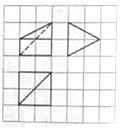19．如图，网格纸上小正方形的边长为1，粗实线及粗虚线画出的是某四棱锥的三视图，则该四棱锥各个侧面中，最大的侧面面积为（　　）
A．2B．$\sqrt{5}$C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网