题目内容
13.已知函数$f(x)=\sqrt{3}sin(x+\frac{π}{4})$,x∈R(1)求f(x)的单调增区间;
(2)已知A、B、C是△ABC的内角,且满足$f(B)=\sqrt{3}$,求$\sqrt{2}$cosA+cosC 的最大值.
分析 (1)利用正弦函数的单调区间,求f(x)的单调增区间;
(2)利用$A+C=\frac{3}{4}π$,将所求式转换,即可求$\sqrt{2}$cosA+cosC 的最大值.
解答 解:(1)令$-\frac{π}{2}+2kπ≤x+\frac{π}{4}≤\frac{π}{2}+2kπ,k∈Z$,得$-\frac{3π}{4}+2kπ≤x≤\frac{π}{4}+2kπ,k∈Z$
∴f(x)的单调增区间是$[-\frac{3π}{4}+2kπ,\frac{π}{4}+2kπ](k∈Z)$…(5分)
(2)$f(B)=\sqrt{3}$,即$sin(B+\frac{π}{4})=1$,因为角B是三角形的内角,所以B=$\frac{π}{4}$…(6分)
∵A+B+C=π,∴$A+C=\frac{3}{4}π$…(7分)
∴$\sqrt{2}cosA+cosC$=$\sqrt{2}cosA+(-\frac{{\sqrt{2}}}{2}cosA)+\frac{{\sqrt{2}}}{2}sinA$=$\frac{{\sqrt{2}}}{2}cosA+\frac{{\sqrt{2}}}{2}sinA$=$sin(A+\frac{π}{4})$(10分)
∵$A+C=\frac{3}{4}π$∴$A\;∈\;(0,\frac{3}{4}π)$…(11分)
∴$A+\frac{π}{4}\;∈\;(\frac{π}{4},π)$…(12分)
∴$sin(A+\frac{π}{4})$最大值为1,即$\sqrt{2}cosA+cosC$最大值为1 …(14分)
点评 本题考查三角函数的图象与性质,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
8.某大学的男生的体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立回归方程$\stackrel{∧}{y}$=0.85x-85.71,则下列结论中不正确的是( )
| A. | y与x具有正的线性相关关系 | |
| B. | 若该大学某女生身高为170cm,则可断定其体重必为58.79kg | |
| C. | 过该大学某女生身高增加1cm,则其体重约增加0.85kg | |
| D. | 回归直线过样本的中心$(\overline x,\overline y)$ |
2.如图,已知ABCD-A′B′C′D′为正方体,则下列结论错误的是( )
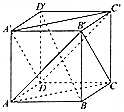

| A. | 平面ACB′∥平面A′C′D | B. | B′C⊥BD′ | ||
| C. | B′C⊥DC′ | D. | BD′⊥平面A′C′D |
3.在△ABC中,角A,B,C的对边分别为a,b,c,且满足sinA=2sinBcosC,则△ABC的形状为( )
| A. | 等腰三角形 | B. | 直角三角形 | C. | 等边三角形 | D. | 等腰直角三角形 |
