题目内容

16．已知集合A={x|x2+2x-3≤0}，B={x|0≤log4（x+2）≤1}，则A∩B=（　　）
A．[-3，2]B．[-1，1]C．[-1，2]D．[1，2]

分析 先分别求出集合A和B，由此利用交集定义能求出A∩B．

解答 解：∵集合A={x|x2+2x-3≤0}={x|-3≤x≤1}，
B={x|0≤log4（x+2）≤1}={x|-1≤x≤2}，
∴A∩B={x|-1≤x≤1}=[-1，1]．
故选：B．

点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集定义的合理运用．

练习册系列答案
相关题目
6．设函数f（x）=lnx+$\frac{a}{x-1}$（a＞0）．
（Ⅰ）当a=$\frac{1}{12}$时，求函数f（x）的单调区间；
（Ⅱ）若函数f（x）在区间（0，$\frac{1}{e}$）内有极值点，当x1∈（0，1），x2∈（1，+∞），求证：f（x2）-f（x1）＞e+2-$\frac{1}{e}$．
7．如图，ABC-A1B1C1是底面边长为2，高为$\frac{\sqrt{3}}{2}$的正三棱柱，经过AB的截面与上
底面相交于PQ，设C1P=λC1A1（0＜λ＜1）．
（1）证明：PQ∥A1B1；
（2）当CF⊥平面ABQP时，在图中作出点C在平面ABQP内的正投影F（说明作法及理由），并求四棱锥CABPQ表面积．
4．已知数列{an}，{bn}前n项和分别为Sn，Tn，an+1-an=2（bn+1-bn），b1=3，Sn=n2+2n+3，则Tn=$\frac{1}{2}$（n2+2n+3）．（n∈N*）．
11．四个不同的小球，全部放入编号为1，2，3，4，5的五个盒子中．（结果写成数字）
（1）1号盒子中有球的放法有多少种？
（2）恰有两个空盒的放法有多少种？
（3）恰有三个空盒的放法有多少种？
（4）甲球所放盒的编号不小于乙球所放盒的编号的放法有多少种？
1．如图，在矩形ABCD中，M是BC的中点，N是CD的中点，若$\overrightarrow{AC}=λ\overrightarrow{AM}+μ\overrightarrow{BN}$，则λμ=$\frac{12}{25}$．
8．某大学的男生的体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立回归方程$\stackrel{∧}{y}$=0.85x-85.71，则下列结论中不正确的是（　　）
A．y与x具有正的线性相关关系
B．若该大学某女生身高为170cm，则可断定其体重必为58.79kg
C．过该大学某女生身高增加1cm，则其体重约增加0.85kg
D．回归直线过样本的中心$（\overline x，\overline y）$
5．已知数列{an}的前n项和为Sn，且Sn=2n（n∈N*）．
（1）求数列{an}的通项公式；
（2）设bn=anlog2an，求{bn}的前n项和Tn．
6．如图是一个空间几何体的三视图，则该几何体的表面积为（　　）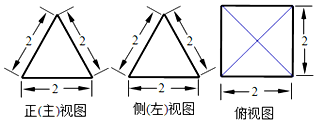 
A．16B．12C．$\frac{4\sqrt{3}}{3}$+4D．4$\sqrt{3}$+4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网