题目内容
已知函数y=f(x)在定义域R上是增函数,值域为(0,+∞),且满足:f(-x)=
.设F(x)=
.
(1)求函数y=F(x)值域和零点;
(2)判断函数y=F(x)奇偶性和单调性,并给予证明.
| 1 |
| f(x) |
| 1-f(x) |
| 1+f(x) |
(1)求函数y=F(x)值域和零点;
(2)判断函数y=F(x)奇偶性和单调性,并给予证明.
考点:函数单调性的判断与证明,函数的值域,函数奇偶性的判断
专题:综合题,函数的性质及应用
分析:(1)确定函数y=F(x)的解析式,利用值域为(0,+∞),即可求函数y=F(x)值域和零点;
(2)利用奇偶性和单调性的定义,即可判断函数y=F(x)奇偶性和单调性.
(2)利用奇偶性和单调性的定义,即可判断函数y=F(x)奇偶性和单调性.
解答:
解:(1)∵f(-x)=
,
∴F(x)=
=-1+
,
∵f(x)>0,∴0<
<1
∴-1<F(x)<1,
故y=F(x)的值域为(-1,1);----------------------------------------(4分)
∵f(-x)=
,
∴令x=0,f(0)=±1,
∵f(x)>0,∴f(0)=1.
故y=F(x)的零点为x=0------------------------------------------------(4分)
(2)对任意的x∈R,F(-x)=
=-
=-F(x),--------(3分)
∴y=F(x)是奇函数.-------------------------------------------(2分)
由已知,y=f(x)在定义域R上是增函数,
∴对任意的x1,x2∈R,x1<x2,都有f(x1)-f(x2)<0.
又F(x1)-F(x2)=
-
=
>0.------------(3分)
∴y=F(x)在定义域R上是减函数.-----------------------------------------------------(2分)
| 1 |
| f(x) |
∴F(x)=
| 1-f(x) |
| 1+f(x) |
| 2 |
| 1+f(x) |
∵f(x)>0,∴0<
| 1 |
| 1+f(x) |
∴-1<F(x)<1,
故y=F(x)的值域为(-1,1);----------------------------------------(4分)
∵f(-x)=
| 1 |
| f(x) |
∴令x=0,f(0)=±1,
∵f(x)>0,∴f(0)=1.
故y=F(x)的零点为x=0------------------------------------------------(4分)
(2)对任意的x∈R,F(-x)=
| 1-f(-x) |
| 1+f(-x) |
| 1-f(x) |
| 1+f(x) |
∴y=F(x)是奇函数.-------------------------------------------(2分)
由已知,y=f(x)在定义域R上是增函数,
∴对任意的x1,x2∈R,x1<x2,都有f(x1)-f(x2)<0.
又F(x1)-F(x2)=
| 2 |
| 1+f(x1) |
| 2 |
| 1+f(x2) |
| f(x2)-f(x1) |
| [1+f(x1)][1+f(x2)] |
∴y=F(x)在定义域R上是减函数.-----------------------------------------------------(2分)
点评:本题考查函数单调性的判断与证明,考查函数的值域,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
平面上满足线性约束条件
的点(x,y)形成的区域为M,区域M关于直线y=2x对称的区域为N,则区域M,N中距离最近的两点间的距离为( )
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
将函数y=sin2x+
cos2x(x∈R)的图象向左平移φ(φ>0)个单位长度后,所得到的一个偶函数的图象,则φ的最小值是( )
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
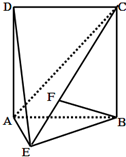 如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
如图,直二面角D-AB-E中,四边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.