Question

平面上满足线性约束条件

x≥2 x+y≤0 x-y-10≤0

的点（x，y）形成的区域为M，区域M关于直线y=2x对称的区域为N，则区域M，N中距离最近的两点间的距离为（　　）

• A、

  6 5

  5

• B、

  12 5

  5

• C、

  8 3

  5

• D、

  16 3

  5

Answer 1

考点：简单线性规划

专题：不等式的解法及应用

分析：作出不等式组对应的平面区域，利用数形结合以及图象对称的性质即可得到结论．

解答： 解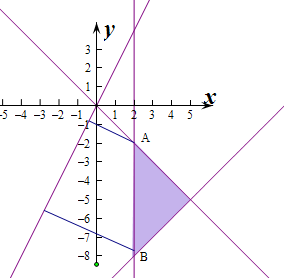：作出不等式组对应的区域M，要使区域M，N中两点间的距离最近，
则根据对称性可知，只要求出区域M内点到直线y=2x的最短距离即可．
由图象可知A到直线y=2x的距离最近，
由

x=2 x+y=0

，解得

x=2 y=-2

，
即A（2，-2），
则A到直线2x-y=0的距离d=

|4-(-2)|

1+22

=

6

5

=

6 5

5

，
即区域M，N中距离最近的两点间的距离为2d=

12 5

5

，
故选：B．

点评：本题主要考查线性规划的应用以及点到直线的距离，利用数形结合是解决本题的关键，考查了转化的思想．