题目内容
若已知数列{an}是首项为6-12t,公差为6的等差数列;数列{bn}的前n项和为Sn=3n-t.
(1)求数列{an}和{bn}的通项公式;
(2)若数列{bn}是等比数列.试证明:对于任意的n(n∈N*,n≥1),均存在正整数cn,使得bn+1=acn,并求数列{cn}的前n项和Tn.
(1)求数列{an}和{bn}的通项公式;
(2)若数列{bn}是等比数列.试证明:对于任意的n(n∈N*,n≥1),均存在正整数cn,使得bn+1=acn,并求数列{cn}的前n项和Tn.
考点:等差数列与等比数列的综合
专题:等差数列与等比数列
分析:(1)利用数列{an}是首项为6-12t,公差为6的等差数列,可求数列{an}的通项公式,利用Sn=3n-t,再写一式,即可求出{bn}的通项公式;
(2)先确定t的值,可得数列的通项,要使bn+1=acn成立,则bn+1=2×3n=6cn-12,利用cn=3n-1+2,而对任意的n(n∈N*,n≥1),3n-1+2为正整数,利用数列的求和公式,即可得出结论.
(2)先确定t的值,可得数列的通项,要使bn+1=acn成立,则bn+1=2×3n=6cn-12,利用cn=3n-1+2,而对任意的n(n∈N*,n≥1),3n-1+2为正整数,利用数列的求和公式,即可得出结论.
解答:
(1)解:∵数列{an}是等差数列,
∴an=(6-12t)+6(n-1)=6n-12t
而数列{bn}的前n项和为Sn=3n-t.
∴当n≥2时,bn=(3n-t)-(3n-1-t)=2×3n-1
∴bn=
(2)证明:∵数列{bn}是等比数列,∴3-t=2×31-1=2,∴t=1
∴an=6n-12,bn=2×3n-1
而bn+1=2×3n,acn=6cn-12,
要使bn+1=acn成立,则bn+1=2×3n=6cn-12,
∴cn=3n-1+2,而对任意的n(n∈N*,n≥1),3n-1+2为正整数
∴对任意的n(n∈N*,n≥1),均存在正整数cn,使得bn+1=acn成立.
∴数列{cn}的前n项和Tn=2n+
=
+2n
∴an=(6-12t)+6(n-1)=6n-12t
而数列{bn}的前n项和为Sn=3n-t.
∴当n≥2时,bn=(3n-t)-(3n-1-t)=2×3n-1
∴bn=
|
(2)证明:∵数列{bn}是等比数列,∴3-t=2×31-1=2,∴t=1
∴an=6n-12,bn=2×3n-1
而bn+1=2×3n,acn=6cn-12,
要使bn+1=acn成立,则bn+1=2×3n=6cn-12,
∴cn=3n-1+2,而对任意的n(n∈N*,n≥1),3n-1+2为正整数
∴对任意的n(n∈N*,n≥1),均存在正整数cn,使得bn+1=acn成立.
∴数列{cn}的前n项和Tn=2n+
| 1×(1-3n) |
| 1-3 |
| 3n-1 |
| 2 |
点评:本题考查数列的通项与求和,考查学生分析解决问题的能力,正确应用等差数列、等比数列的通项公式是关键.

练习册系列答案
相关题目
曲线y=cosx(0≤x≤
π)与x轴以及直线x=
所围图形的面积为( )
| 3 |
| 2 |
| 3π |
| 2 |
| A、4 | ||
| B、2 | ||
C、
| ||
| D、3 |
 如图所示,用篱笆围成一个一边靠墙的矩形菜园,假设墙有足够长.
如图所示,用篱笆围成一个一边靠墙的矩形菜园,假设墙有足够长.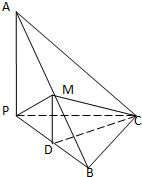 如图,已知三棱锥A-PBC中,AC⊥BC,AP⊥PC,M为AB的中点,D为PB的中点,且△PMB为正三角形.
如图,已知三棱锥A-PBC中,AC⊥BC,AP⊥PC,M为AB的中点,D为PB的中点,且△PMB为正三角形.