题目内容
设f(x)对任意的x,y有f(x+y)=f(x)+f(y),且当x>0时,f(x)<0.
(1)求证f(x)是R上的减函数;
(2)若f(1)=-
,求f(x)在[2,3]上的最大值和最小值.
(1)求证f(x)是R上的减函数;
(2)若f(1)=-
| 2 |
| 3 |
考点:抽象函数及其应用,函数单调性的判断与证明,函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)采用赋值法,先将f(x+y)=f(x)+f(y)变形为f(x+y)-f(x)=f(y),再结合函数单调性的定义式f(x2)-f(x1)合理赋值,结合且当x>0时,f(x)<0判断差的符号,解决问题.
(2)结合单调性,f(2),f(3)分别是最大值、最小值,再利用f(x+y)=f(x)+f(y)结合f(1)的值求解.
(2)结合单调性,f(2),f(3)分别是最大值、最小值,再利用f(x+y)=f(x)+f(y)结合f(1)的值求解.
解答:
解:(1)因为f(x+y)=f(x)+f(y),所以f(x+y)-f(x)=f(y),
则任取x1<x2,有f(x2)-f(x1)=f(x2-x1),
又因为当x>0时,f(x)<0,且x2-x1>0,
所以f(x2-x1)<0,即f(x2)-f(x1)<0
所以f(x2)<f(x1),所以函数f(x)是减函数.
(2)结合(1)可知,函数f(x)在[2,3]上是减函数,
结合f(x+y)=f(x)+f(y),
所以ymin=f(3)=f(2)+f(1)=f(1)+f(1)+f(1)=3f(1)=3×(-
)=-2,
ymax=f(2)=f(1)+f(1)=2f(1)=2×(-
)=-
.
所以该函数在[2,3]上的最大值为f(2)=-2,最小值为f(3)=-
.
则任取x1<x2,有f(x2)-f(x1)=f(x2-x1),
又因为当x>0时,f(x)<0,且x2-x1>0,
所以f(x2-x1)<0,即f(x2)-f(x1)<0
所以f(x2)<f(x1),所以函数f(x)是减函数.
(2)结合(1)可知,函数f(x)在[2,3]上是减函数,
结合f(x+y)=f(x)+f(y),
所以ymin=f(3)=f(2)+f(1)=f(1)+f(1)+f(1)=3f(1)=3×(-
| 2 |
| 3 |
ymax=f(2)=f(1)+f(1)=2f(1)=2×(-
| 2 |
| 3 |
| 4 |
| 3 |
所以该函数在[2,3]上的最大值为f(2)=-2,最小值为f(3)=-
| 4 |
| 3 |
点评:抽象函数的单调性问题只能用定义,因此要合理对已知等式中的x,y合理赋值,变换出f(x2)-f(x1)=f(x2-x1)是解题的关键.已知特定的函数再求值的问题,一般是赋值法.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
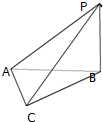 如图,PB⊥平面ABC,△ABC为直角三角形,PB=BC=AC,∠ACB=90°.
如图,PB⊥平面ABC,△ABC为直角三角形,PB=BC=AC,∠ACB=90°.