题目内容
平面内区域M=
的面积可用函数f(k)表示,若f(k)=8,则k等于( )
|
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:简单线性规划的应用,简单线性规划
专题:不等式的解法及应用
分析:画出约束条件表示的可行域,通过f(k)=8,得到k的方程,求解即可.
解答:
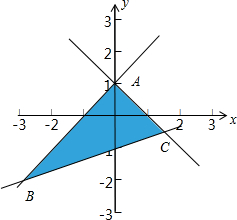 解:约束条件
解:约束条件
表示的可行域如图阴影部分,kx-y-1=0表示过(0,-1)的直线系,由图形可知A(0,1),
解得
,B(
,
).
由
,解得
,C(
,
).
平面内区域M=
的面积可用函数f(k)=
×2×|xB||xC|=
=8.
解得:k=
.
故选:D.
 解:约束条件
解:约束条件
|
|
|
|
| 2 |
| k-1 |
| k+1 |
| k-1 |
由
|
|
| 2 |
| k+1 |
| k-1 |
| k+1 |
平面内区域M=
|
| 1 |
| 2 |
| 4 |
| 1-k2 |
解得:k=
| ||
| 2 |
故选:D.
点评:本题考查线性规划的应用,转化思想以及计算能力,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
设k<-1,则关于x、y的方程(1-k)x2+y2=k2-1所表示的曲线是( )
| A、实轴在x轴上的双曲线 |
| B、实轴在y轴上的双曲线 |
| C、长轴在x轴上的椭圆 |
| D、长轴在y轴上的椭圆 |
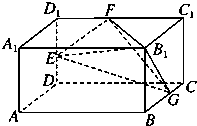 如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.
如图,长方体AC1中,AB=2,BC=AA1=1.E、F、G分别为棱DD1、D1C1、BC的中点.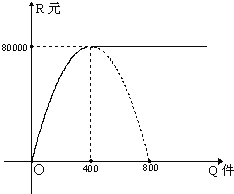 某工厂生产某种产品,固定成本为20000元,每生产一件产品,成本增加100元.已知总收益R是年产量Q(件)的函数,其图象(图中实线部分)如下:当年产量Q在[0,400]内时,为抛物线的一段;当年产量Q>400件时,为一条射线.
某工厂生产某种产品,固定成本为20000元,每生产一件产品,成本增加100元.已知总收益R是年产量Q(件)的函数,其图象(图中实线部分)如下:当年产量Q在[0,400]内时,为抛物线的一段;当年产量Q>400件时,为一条射线.