题目内容
设k＜-1，则关于x、y的方程（1-k）x2+y2=k2-1所表示的曲线是（ ）
| A、实轴在x轴上的双曲线 |
| B、实轴在y轴上的双曲线 |
| C、长轴在x轴上的椭圆 |
| D、长轴在y轴上的椭圆 |
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：根据条件，1-k＞2＞1，k2-1＞0，结合椭圆的标准方程的特征判断曲线的类型．
解答：
解：∵k＜-1，∴1-k＞2＞1，k2-1＞0，
∴方程（1-k）x2+y2=k2-1表示实轴在y轴上的椭圆，
故选D．
∴方程（1-k）x2+y2=k2-1表示实轴在y轴上的椭圆，
故选D．
点评：本题考查椭圆的标准方程的特征，比较基础．
练习册系列答案
名师指导期末冲刺卷系列答案
相关题目
P为双曲线
-
=1（a＞0，b＞0）上的一点，F1，F2 为其左右两焦点．若∠PF1F2=120°，且F1 F2=PF1，则双曲线的离心率为（ ）
| x 2 |
| a 2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
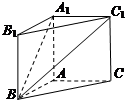在直三棱柱（侧棱垂直底面）ABC-A1B1C1中，AB=AC=1，∠BAC=90°，且异面直线A1B与B1C1所成的角等于60°．