题目内容

在研究色盲与性别的关系调查中，调查了男性240人，其中有19人患色盲，调查的260个女性中3人患色盲
（1）根据以上的数据建立一个2*2的列联表；
（2）若认为“性别与患色盲有关系”，则出错的概率会是多少．
考点：独立性检验的应用
专题：计算题,概率与统计
分析：（1）根据调查了男性240人，其中有19人患色盲，调查的260个女性中3人患色盲，列出列联表；
（2）代入公式计算得出K2值，结合临界值，即可求得结论．
解答： 解：（1）
 患色盲不患色盲总计
男19221240
女3257260
总计22478500
（2）假设 H：“性别与患色盲没有关系”
先算出K的观测值：k2=
500×(19×257-221×3)2
240×260×22×478
≈13.569    9分
则若认为“性别与患色盲有关系”，则出错的概率为0.001   12分
点评：本题考查独立性检验的应用，本题解题的关键是理解临界值对应的概率的意义，能够看出两个变量之间的关系，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=loga（1-x）+loga（x+3）（0＜a＜1）．
（1）求函数f（x）的定义域；
（2）求函数f（x）的零点；
（3）若函数f（x）的最小值为-2，求a的值．
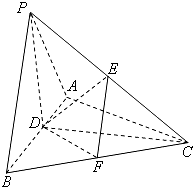如图，在三棱锥P-ABC中，△PAB是等边三角形，D、E分别为AB、PC的中点．
（1）若点F在BC边上，BF=λBC，则实数λ为何值时，PB∥平面DEF；
（2）若∠PAC=∠PBC=90°，AB=2，AC=
5
，求三棱锥P-ABC的体积．
已知数列{an}的前n项和是Sn，且-1，Sn，an+1成等差数列（n∈N*），a1=1．
（1）求数列{an}的通项公式．
（2）若数列{bn}满足b1=a1，bn+1=bn+
1
3an
（n≥1）求数列{bn}的前n项和Tn．
（3）函数f（x）=log3x，设数列{cn}满足cn=
1
(n+3)[f(an)+2]
求数列{cn}的前n项和Rn．
已知（1-2x）2014=a0+a1x+a2x2+…+a2014x2014，则a1+2a2+3a3+…+2014a2014=
 
．
已知△ABC的三内角A，B，C所对的边分别为a，b，c，a=
15
，b=2，向量
m
=（-1，
3
），
n
=（cosA，sinA），且
m
•
n
=1．
（1）求角A；
（2）求
1+sin2B
cos2B-sin2B
的值．
已知函数f（x）=2cos（2x+
π
6
）
（1）当-
π
6
≤x≤
π
3
时，求函数y=f（x）的最大值和最小值及相应的x的值；
（2）若方程f（x）=a在区间[0，
2π
3
]上只有一个实数根，求实数a的取值集合．
已知数列{an}为等差数列，a3=5，a7=13，数列{bn}的前n项和为Sn，且有Sn=2bn-1．
1）求{an}、{bn}的通项公式；
2）若cn=anbn，{cn}的前n项和为Tn，求Tn．
已知函数f（x）=
1
x
-alnx．（a∈R）
（1）当a=-1时，试确定函数f（x）在其定义域内的单调性；
（2）求函数f（x）在（0，e）上的最小值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网