题目内容
△ABC中，求证：
+
+
=0．
| a2-b2 |
| cosA+cosB |
| b2-c2 |
| cosB+cosC |
| c2-a2 |
| cosC+cosA |
考点：余弦定理
专题：解三角形
分析：利用正弦定理可得
=
=
=2R≠0，a2-b2=4R2（sin2A-sin2B）=4R2（cos2B-cos2A），同理可得b2-c2=4R2（cos2C-cos2B），c2-a2=4R2（cos2A-cos2C），代入等式的左边化简即可证明．
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
解答：
证明：由正弦定理可得
=
=
=2R≠0，
∴a2-b2=4R2（sin2A-sin2B）=4R2[1-cos2A-（1-cos2B）]=4R2（cos2B-cos2A），
同理可得b2-c2=4R2（cos2C-cos2B），c2-a2=4R2（cos2A-cos2C），
∴左边=4R2[（cosB-cosA）+（cosC-cosB）+（cosA-cosC）]=0=右边．
∴
+
+
=0．
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
∴a2-b2=4R2（sin2A-sin2B）=4R2[1-cos2A-（1-cos2B）]=4R2（cos2B-cos2A），
同理可得b2-c2=4R2（cos2C-cos2B），c2-a2=4R2（cos2A-cos2C），
∴左边=4R2[（cosB-cosA）+（cosC-cosB）+（cosA-cosC）]=0=右边．
∴
| a2-b2 |
| cosA+cosB |
| b2-c2 |
| cosB+cosC |
| c2-a2 |
| cosC+cosA |
点评：本题考查了正弦定理的应用、同角三角函数基本关系式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
方程x3-x-3=0的实数解落在的区间是（ ）
| A、[-1，0] |
| B、[0，1] |
| C、[1，2] |
| D、[2，3] |
函数f（x）=|sinx|+2|cosx|的值域为（ ）
A、[1，
| ||
| B、[1，2] | ||
C、[2，
| ||
D、[
|
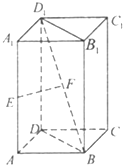如图，已知棱柱ABCD-A1B1C1D1的底面是正方形，且AA1⊥平面ABCD，E为棱AA1的中点，F为线段BD1的中点．