题目内容
某公司研发甲、乙两种新产品,根据市场调查预测,甲产品的利润y(单位:万元)与投资x(单位:万元)满足:f(x)=alnx-bx+3(a,b∈R,a,b为常数),且曲线y=f(x)与直线y=kx在(1,3)点相切;乙产品的利润与投资的算术平方根成正比,且其图象经过点(4,4).
(I)分别求甲、乙两种产品的利润与投资资金间的函数关系式;
(Ⅱ)已知该公司已筹集到40万元资金,并将全部投入甲、乙两种产品的研发,每种产品投资均不少于10万元.问怎样分配这40万元投资,才能使该公司获得最大利润?其最大利润约为多少万元?
(参考数据:ln=10=2.303,ln15=2.708,ln20=2.996,ln25=3.219,ln30=3.401)
(I)分别求甲、乙两种产品的利润与投资资金间的函数关系式;
(Ⅱ)已知该公司已筹集到40万元资金,并将全部投入甲、乙两种产品的研发,每种产品投资均不少于10万元.问怎样分配这40万元投资,才能使该公司获得最大利润?其最大利润约为多少万元?
(参考数据:ln=10=2.303,ln15=2.708,ln20=2.996,ln25=3.219,ln30=3.401)
考点:函数模型的选择与应用
专题:函数的性质及应用
分析:(I)根据条件分别求出a,b,即可求出甲、乙两种产品的利润与投资资金间的函数关系式;
(Ⅱ)设甲产品投资x万元,则乙产品投资(40-x)万元,建立函数关系,求函数的导数,利用导数研究函数的最值即可.
(Ⅱ)设甲产品投资x万元,则乙产品投资(40-x)万元,建立函数关系,求函数的导数,利用导数研究函数的最值即可.
解答:
解:(I)函数的定义域为(0,+∞),
函数的导数为f′(x)=
-b,
∵(1,3)在直线y=kx上,
∴k=3,
∵曲线y=f(x)与直线y=kx在(1,3)点相切,
∴
,解得
,
即甲产品的利润y与投资x的关系式:f(x)=3lnx+3,
乙产品的利润与投资资金间的函数关系式g(x)=m•
;
将(4,4)代入函数g(x)得
m=4,解得m=2.
故g(x)=2
,(x>0).
(Ⅱ)设甲产品投资x万元,则乙产品投资(40-x)万元,且x∈[10,30],
则该公司所得利润为:y=3lnx+3+2
,
则函数的导数f′(x)=
-
,
由f′(x)>0得10≤x<15,
由f′(x)<0得15<x≤30,
即当x=15时,函数取得极大值,同时也是最大值,
即最大值为y=3ln15+3+2
=3×2.708+13=21.124万元.
故当甲产品投资15万元,则乙产品投资25万元时,公司取得最大利润,最大利润为21.124万元.
函数的导数为f′(x)=
| a |
| x |
∵(1,3)在直线y=kx上,
∴k=3,
∵曲线y=f(x)与直线y=kx在(1,3)点相切,
∴
|
|
即甲产品的利润y与投资x的关系式:f(x)=3lnx+3,
乙产品的利润与投资资金间的函数关系式g(x)=m•
| x |
将(4,4)代入函数g(x)得
| 4 |
故g(x)=2
| x |
(Ⅱ)设甲产品投资x万元,则乙产品投资(40-x)万元,且x∈[10,30],
则该公司所得利润为:y=3lnx+3+2
| 40-x |
则函数的导数f′(x)=
| 3 |
| x |
| 1 | ||
|
由f′(x)>0得10≤x<15,
由f′(x)<0得15<x≤30,
即当x=15时,函数取得极大值,同时也是最大值,
即最大值为y=3ln15+3+2
| 40-15 |
故当甲产品投资15万元,则乙产品投资25万元时,公司取得最大利润,最大利润为21.124万元.
点评:本题主要考查函数的应用问题,利用导数研究函数的最值是解决本题的关键.考查导数的优化问题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
设a=log
5,b=3
,c=(
)0.3,则有( )
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 5 |
| A、a<b<c |
| B、c<b<a |
| C、a<c<b |
| D、c<a<b |
已知函数f(x)=
-lnx,则有下列结论中错误的是( )
| lnx |
| 1+x |
| A、?x0∈R,f(x)=0 | ||
| B、若x0是f(x)的最大值点,则f(x0)=x0 | ||
C、若x0是f(x)的最大值点,则f(x0)<
| ||
| D、若x0是f(x)的极大值点,则f(x)在(x0,+∞)上单调递增 |
设函数f(x)=
若f(f(t))≤2,则实数t的取值范围是( )
|
A、(-∞,
| ||
B、[
| ||
| C、(-∞,-2] | ||
| D、[-2,+∞) |
执行如图所示的程序框图,输出的s值为( )
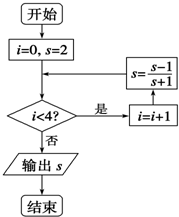

| A、-3 | ||
B、-
| ||
| C、2 | ||
D、
|
 如图所示,已知双曲线的中心在坐标原点O,焦点分别是F1(-2,0),且双曲线经过点P(2,3).
如图所示,已知双曲线的中心在坐标原点O,焦点分别是F1(-2,0),且双曲线经过点P(2,3).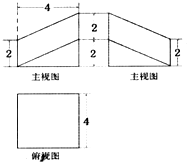 棱长为4的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是
棱长为4的正方体被一平面截成两个几何体,其中一个几何体的三视图如图所示,那么该几何体的体积是