题目内容
若函数f（x）=
-a是奇函数，则实数a的值为 ．
| 2 |
| 3x+1 |
考点：函数奇偶性的性质
专题：函数的性质及应用
分析：根据奇函数的结论：f（0）=0列出方程，求出a的值即可．
解答：
解：因为奇函数f（x）=
-a的定义域是R，
所以f（0）=
-a=0，解得a=1，
故答案为：1．
| 2 |
| 3x+1 |
所以f（0）=
| 2 |
| 30+1 |
故答案为：1．
点评：本题考查奇函数的性质的应用，属于基础题．
练习册系列答案
相关题目
函数f1（x）=
，f2（x）=
，…，fn+1（x）=
，…，则函数f2015（x）是（ ）
| 1 |
| x |
| 1 |
| x+f1(x) |
| 1 |
| x+fn(x) |
| A、奇函数但不是偶函数 |
| B、偶函数但不是奇函数 |
| C、既是奇函数又是偶函数 |
| D、既不是奇函数又不是偶函数 |
函数f（x）=log2（x+1）的定义域为（ ）
| A、（0，+∞） |
| B、[-1，+∞） |
| C、（-1，+∞） |
| D、（1，+∞） |
x，y满足约束条件
，若z=y-2ax取得最大值的最优解不唯一，则实数a的值为（ ）
|
A、1或-
| ||
B、
| ||
| C、2或1 | ||
| D、2或-1 |
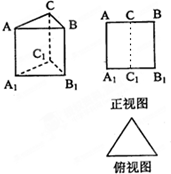如图，水平放置的三棱柱的侧棱长和底边长均为2，且侧棱AA1⊥面A1B1C1，正视图是边长为2的正方形，俯视图为一个等边三角形，该三棱柱的左视图面积为（ ）
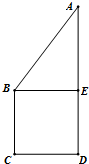如图正方形BCDE的边长为a，已知AB=已知△ABC是等腰三角形，∠ABC=120°，以A，B为焦点的双曲线过点C，则双曲线的离心率为（ ）
A、1+
| ||||
B、1+
| ||||
C、
| ||||
D、
|