题目内容
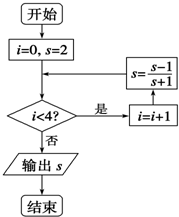
执行如图所示的程序框图，输出的s值为（ ）
| A、-3 | ||
B、-
| ||
| C、2 | ||
D、
|
考点：循环结构
专题：图表型,算法和程序框图
分析：执行程序框图，依次写出每次循环得到的i，s的值，当i=4时，不满足条件i＜4，退出循环，输出s的值为2．
解答：
解：执行程序框图，可得
i=0，s=2
满足条件i＜4，i=1，s=
满足条件i＜4，i=2，s=-
满足条件i＜4，i=3，s=-3
满足条件i＜4，i=4，s=2
不满足条件i＜4，退出循环，输出s的值为2．
故选：C．
i=0，s=2
满足条件i＜4，i=1，s=
| 1 |
| 3 |
满足条件i＜4，i=2，s=-
| 1 |
| 2 |
满足条件i＜4，i=3，s=-3
满足条件i＜4，i=4，s=2
不满足条件i＜4，退出循环，输出s的值为2．
故选：C．
点评：本题主要考察了程序框图和算法，每次循环正确得到s的值是解题的关键，属于基础题．
练习册系列答案
相关题目
已知△ABC是等腰三角形，∠ABC=120°，以A，B为焦点的双曲线过点C，则双曲线的离心率为（ ）
A、1+
| ||||
B、1+
| ||||
C、
| ||||
D、
|
已知函数f（x）=
，其中a∈R，若对任意的非零的实数x1，存在唯一的非零的实数x2（x2≠x1），使得f（x2）=f（x1）成立，则k的最大值为（ ）
|
| A、-1 | B、-2 | C、-4 | D、-3 |
若函数f（x）为偶函数，x＞0时，f（x）单调递增，P=f（-π），Q=f（e），R=f（
），则P，Q，R的大小为（ ）
| 2 |
| A、R＞Q＞P |
| B、Q＞R＞P |
| C、P＞R＞Q |
| D、P＞Q＞R |
圆x2+y2-2y-1=0关于直线y=x对称的圆的方程是（ ）
| A、（x-1）2+y2=2 |
| B、（x+1）2+y2=2 |
| C、（x-1）2+y2=22 |
| D、（x+1）2+y2=22 |
若关于x的方程2x=a2有负实数根，则实数a的取值范围是（ ）
| A、（-1，1） |
| B、（-∞，0）∪（0，+∞） |
| C、（-1，0）∪（0，1） |
| D、（-∞，-1）∪（1，+∞） |