题目内容
已知函数f(x)=
-lnx,则有下列结论中错误的是( )
| lnx |
| 1+x |
| A、?x0∈R,f(x)=0 | ||
| B、若x0是f(x)的最大值点,则f(x0)=x0 | ||
C、若x0是f(x)的最大值点,则f(x0)<
| ||
| D、若x0是f(x)的极大值点,则f(x)在(x0,+∞)上单调递增 |
考点:利用导数研究函数的单调性
专题:计算题,导数的综合应用
分析:先求函数f(x)=
-lnx的定义域为(0,+∞),再求导并化简f′(x)=
(
-1)-lnx
=-
;从而对四个选项判断即可.
| lnx |
| 1+x |
| 1 |
| x |
| 1 |
| 1+x |
| 1 |
| (1+x)2 |
| lnx+x+1 |
| (1+x)2 |
解答:
解:函数f(x)=
-lnx的定义域为(0,+∞),
f′(x)=
(
-1)-lnx
=-
;
∵f(1)=0,故A正确;
∵令y=lnx+x+1,
则存在x0∈(0,
),使lnx0+x0+1=0;
又∵y=lnx+x+1是增函数,
故函数f(x)=
-lnx在(0,x0)上是增函数,在(x0,+∞)上是减函数;
故当x=x0时,f(x)有最大值为f(x0)=ln(x0)(
-1)=x0;故B正确;
由以上分析知,C正确;
D不正确;
故选D.
| lnx |
| 1+x |
f′(x)=
| 1 |
| x |
| 1 |
| 1+x |
| 1 |
| (1+x)2 |
=-
| lnx+x+1 |
| (1+x)2 |
∵f(1)=0,故A正确;
∵令y=lnx+x+1,
则存在x0∈(0,
| 1 |
| 2 |
又∵y=lnx+x+1是增函数,
故函数f(x)=
| lnx |
| 1+x |
故当x=x0时,f(x)有最大值为f(x0)=ln(x0)(
| 1 |
| 1+x0 |
由以上分析知,C正确;
D不正确;
故选D.
点评:本题考查了导数的综合应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
函数f(x)=log2(x+1)的定义域为( )
| A、(0,+∞) |
| B、[-1,+∞) |
| C、(-1,+∞) |
| D、(1,+∞) |
若x2+6<5x,y=x2+5x+6,则有( )
| A、y为任意实数 |
| B、0<y<20 |
| C、20<y<30 |
| D、y>30 |
已知△ABC是等腰三角形,∠ABC=120°,以A,B为焦点的双曲线过点C,则双曲线的离心率为( )
A、1+
| ||||
B、1+
| ||||
C、
| ||||
D、
|
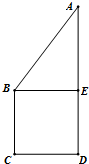 如图正方形BCDE的边长为a,已知AB=
如图正方形BCDE的边长为a,已知AB=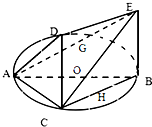 如图,一简单几何体ABCDE的一个面ABC内接于圆O,G、H分别是AE、BC的中点,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.
如图,一简单几何体ABCDE的一个面ABC内接于圆O,G、H分别是AE、BC的中点,AB是圆O的直径,四边形DCBE为平行四边形,且DC⊥平面ABC.