题目内容
设P是双曲线
-
=1右支上的任意一点,经过点P的直线与双曲线的渐近线分别交于A、B两点,△AOB的面积是9.且
=λ
(λ>0),则λ的值是 .
| x2 |
| 4 |
| y2 |
| 16 |
| AP |
| PB |
考点:双曲线的简单性质
专题:计算题,平面向量及应用,直线与圆,圆锥曲线的定义、性质与方程
分析:求出双曲线的渐近线方程,设P(x,y),A(x1,y1),B(x2,y2),则y1=2x1,y2=-2x2,运用定比分点坐标公式,得到x,y的关系式,再代入双曲线方程,求得|OA|,|OB|,再求两渐近线的夹角的正弦,由三角形的面积公式,解方程即可求得λ的值.
解答:
解:双曲线
-
=1的渐近线方程为y=±2x,
设P(x,y),A(x1,y1),B(x2,y2),
则y1=2x1,y2=-2x2,
∵
=λ
(λ>0),
∴x=
,y=
=
=2•
,
由点P(x,y)在双曲线
-
=1(a>0,b>0)上,
∴
-
=1,
化简得:x1x2=
,
又|OA|=
=
|x1|,同理可得|OB|=
|x2|,
∴|OA|•|OB|=5|x1|•|x2|=5•
,
设直线OA与OB所成的夹角为2θ,∵tanθ=
=2,
∴tan2θ=
=
=-
,
∴sin2θ=
=
,
∴S△AOB=
•|OA|•|OB|sin2θ=
×5•
×
=2•
=9,
解得,λ=
或2.
故答案为:
或2.
| x2 |
| 4 |
| y2 |
| 16 |
设P(x,y),A(x1,y1),B(x2,y2),
则y1=2x1,y2=-2x2,
∵
| AP |
| PB |
∴x=
| x1+λx2 |
| 1+λ |
| y1+λy2 |
| 1+λ |
| 2x1-2λx2 |
| 1+λ |
| x1-λx2 |
| 1+λ |
由点P(x,y)在双曲线
| x2 |
| 4 |
| y2 |
| 16 |
∴
| (x1+λx2)2 |
| 4(1+λ)2 |
| (x1-λx2)2 |
| 4(1+λ)2 |
化简得:x1x2=
| (1+λ)2 |
| λ |
又|OA|=
| x12+4x12 |
| 5 |
| 5 |
∴|OA|•|OB|=5|x1|•|x2|=5•
| (1+λ)2 |
| λ |
设直线OA与OB所成的夹角为2θ,∵tanθ=
| 4 |
| 2 |
∴tan2θ=
| 2tanθ |
| 1-tan2θ |
| 2×2 |
| 1-4 |
| 4 |
| 3 |
∴sin2θ=
| 4 | ||
|
| 4 |
| 5 |
∴S△AOB=
| 1 |
| 2 |
| 1 |
| 2 |
| (1+λ)2 |
| λ |
| 4 |
| 5 |
| (1+λ)2 |
| λ |
解得,λ=
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题考查双曲线的标准方程与性质的综合应用,考查直线与圆锥曲线的位置关系,考查运算能力,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
若x2+6<5x,y=x2+5x+6,则有( )
| A、y为任意实数 |
| B、0<y<20 |
| C、20<y<30 |
| D、y>30 |
圆x2+y2-2y-1=0关于直线y=x对称的圆的方程是( )
| A、(x-1)2+y2=2 |
| B、(x+1)2+y2=2 |
| C、(x-1)2+y2=22 |
| D、(x+1)2+y2=22 |
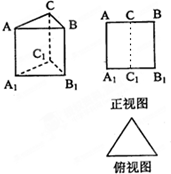 如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥面A1B1C1,正视图是边长为2的正方形,俯视图为一个等边三角形,该三棱柱的左视图面积为( )
如图,水平放置的三棱柱的侧棱长和底边长均为2,且侧棱AA1⊥面A1B1C1,正视图是边长为2的正方形,俯视图为一个等边三角形,该三棱柱的左视图面积为( )