题目内容
设f（x）=x2-4x+3，x∈[1，4]，则f（x）的最小值为（ ）
| A、-1 | B、0 | C、3 | D、-2 |
考点：二次函数在闭区间上的最值
专题：函数的性质及应用
分析：根据函数在[1，4]上的图象和性质，即可求最小值．
解答：
解：y=（x-2）2-1，
∵函数的图象开口向上，顶点是（2，-1），2∈[1，4]，
∴函数的最小值为f（2）=-1，
故选：A．
∵函数的图象开口向上，顶点是（2，-1），2∈[1，4]，
∴函数的最小值为f（2）=-1，
故选：A．
点评：本题考查了函数最小值的求法，利用函数的图象求函数的最值是常用方法，属于基础题．
练习册系列答案
相关题目
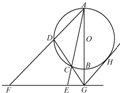如图，AB是圆O的直径，G是AB延长线上的一点，GCD是圆O的割线，过点G作AG的垂线，交直线AC于点E，交直线 AD于点F，过点G作圆O的切线，切点为H．下列选项中是单调函数的为（ ）
| A、y=tanx | ||
B、y=x-
| ||
| C、y=lg（2x+1） | ||
| D、y=2|x| |