题目内容
若f(x)=
sinωx•cosωx-cos2ωx(ω>0)的周期为
.
(1)求ω的值;
(2)求函数的单调递增区间.
| 3 |
| π |
| 2 |
(1)求ω的值;
(2)求函数的单调递增区间.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:(1)由题意,先化简解析式为f(x)=sin(2ωx-
)-
,再由周期公式求ω的值;
(2)令2kπ-
≤2x-
≤2kπ+
,解之即可得出函数的单调增区间.
| π |
| 6 |
| 1 |
| 2 |
(2)令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
解答:
解:f(x)=
sinωx•cosωx-cos2ωx=
sin2ωx-
=sin(2ωx-
)-
,
(1)f(x)=
sinωx•cosωx-cos2ωx(ω>0)的周期为
,所以
=π,解得ω的值为1;
(2)由(1)知,函数为f(x)=sin(2x-
)-
,
令2kπ-
≤2x-
≤2kπ+
,解得kπ-
≤x≤kπ+
,
即函数的单调递增区间为[kπ-
,kπ+
]k∈z.
| 3 |
| ||
| 2 |
| 1+cos2ωx |
| 2 |
| π |
| 6 |
| 1 |
| 2 |
(1)f(x)=
| 3 |
| π |
| 2 |
| 2π |
| 2ω |
(2)由(1)知,函数为f(x)=sin(2x-
| π |
| 6 |
| 1 |
| 2 |
令2kπ-
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 3 |
即函数的单调递增区间为[kπ-
| π |
| 6 |
| π |
| 3 |
点评:本题考查三角恒等变换及三角函数的周期求解公式,复合三角函数单调区间的求法,属于三角函数基本题,难度不大.避免计算出错,是得分的关键.

练习册系列答案
相关题目
设f(x)=x2-4x+3,x∈[1,4],则f(x)的最小值为( )
| A、-1 | B、0 | C、3 | D、-2 |
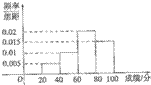 某班的全体学生参加某项技能测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],若不低于80分的人数是8,则该班的学生人数是( )
某班的全体学生参加某项技能测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100],若不低于80分的人数是8,则该班的学生人数是( )