题目内容

下列选项中是单调函数的为（　　）
A、y=tanx
B、y=x-
1
x
C、y=lg（2x+1）
D、y=2|x|
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：分别对A，B，C，D各个选项进行分析，从而得出结论．
解答： 解：对于A：y=tanx，在（kπ-
π
2
，kπ+
π
2
）单调递增，在整个定义域上不具有单调性，
对于B：y′=
x2+1
x2
＞0，在（-∞，0）和（0，+∞）单调递增，在整个定义域上不具有单调性，
对于C：y=lg（2x+1），定义域为：（-
1
2
，+∞），在定义域上单调递增，
对于D：y=2|x|是偶函数，图象关于y轴对称，在整个定义域上不具有单调性，
故选：C．
点评：本题考查了函数的单调性问题，考查了指数函数，对数函数的性质，是一道基础题．
练习册系列答案
相关题目
椭圆的两焦点坐标分别为F1（-
3
，0），F2（
3
，0），且椭圆过点P（1，-
3
2
）．
（1）求椭圆方程；
（2）若 A为椭圆的左顶点，作AM⊥AN与椭圆交于两点M、N，试问：直线MN是否恒过x轴上的一个定点？若是，求出该点坐标；若不是，请说明理由．
设f（x）=x2-4x+3，x∈[1，4]，则f（x）的最小值为（　　）
A、-1B、0C、3D、-2
已知△ABC的顶点A（5，1），AB边上的中线CM所在直线方程为2x-y-5=0，AC边上的高BH所在直线方程为x-2y-5=0．
（1）求AC边所在直线方程；
（2）求顶点C的坐标；
（3）求直线BC的方程．
已知函数f（x）=ax2+bx+1（a，b为实数，a≠0，x∈R）．
（1）若函数f（x）的图象过点（-2，1），且方程f（x）=0有且只有一个根，求f（x）的表达式；
（2）在（1）的条件下，当x∈[-1，2]时，g（x）=f（x）-kx是单调函数，求实数k的取值范围．
已知a＞0，b＞0，a+b=1，则(a+
1
a
)(b+
1
b
)的最小值是
 
．
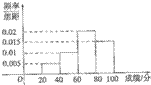某班的全体学生参加某项技能测试，成绩的频率分布直方图如图，数据的分组依次为：[20，40），[40，60），[60，80），[80，100]，若不低于80分的人数是8，则该班的学生人数是（　　）
A、45B、50C、55D、60
（坐标系与参数方程选做题）曲线C1：
x=1+cosθ
y=sinθ
（θ为参数）上的点到曲线C2：
x=-2
2
+
1
2
t 
y=1-
1
2
t 
（t为参数）上的点的最近距离为
 
．
函数f(
x
+1)=x，则函数f（x）=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网