题目内容
12．执行如图所示的程序框图，输出的s=（ ）
| A． | 5 | B． | 20 | C． | 60 | D． | 120 |
分析 先根据已知循环条件和循环体判定循环的规律，然后根据运行的情况判断循环的次数，从而得出所求．
解答 解：第一次循环，s=1，a=5≥3，s=5，a=4；
第二次循环，a=4≥3，s=20，a=3；
第三次循环，a=3≥3，s=60，a=2，
第四次循环，a=2＜3，输出s=60，
故选：C．
点评 本题主要考查了循环结构，循环结构有两种形式：当型循环结构和直到型循环结构，考查分析问题解决问题的能力，属于基础题．新课改地区高考常考题型．
练习册系列答案
相关题目
2．已知等差数列{an}中，Sn为其前n项和，S4=π（其中π为圆周率），a4=2a2，现从此数列的前30项中随机选取一个元素，则该元素的余弦值为负数的概率为（ ）
| A． | $\frac{7}{15}$ | B． | $\frac{1}{2}$ | C． | $\frac{8}{15}$ | D． | $\frac{7}{30}$ |
3．已知抛物线y2=20x的焦点F恰好为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个焦点，且点F到双曲线的渐近线的距离是4，则双曲线的方程为（ ）
| A． | $\frac{{x}^{2}}{41}$$-\frac{{y}^{2}}{16}$=1 | B． | $\frac{{x}^{2}}{21}$$-\frac{{y}^{2}}{4}$=1 | C． | $\frac{{x}^{2}}{3}$$-\frac{{y}^{2}}{4}$=1 | D． | $\frac{{x}^{2}}{9}$$-\frac{{y}^{2}}{16}$=1 |
20．若α∈（$\frac{π}{2}$，π），则3cos2α=cos（$\frac{π}{4}$+α），则sin2α的值为（ ）
| A． | $\frac{1}{18}$ | B． | -$\frac{1}{18}$ | C． | $\frac{17}{18}$ | D． | -$\frac{17}{18}$ |
7．
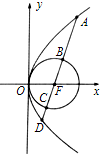如图，抛物线y2=2px（p＞0）和圆x2+y2-px=0，直线l经过抛物线的焦点，依次交抛物线与圆于A，B，C，D四点，|AB|•|CD|=2则p的值为（ ）
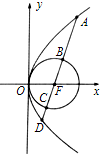如图，抛物线y2=2px（p＞0）和圆x2+y2-px=0，直线l经过抛物线的焦点，依次交抛物线与圆于A，B，C，D四点，|AB|•|CD|=2则p的值为（ ）| A． | $\frac{\sqrt{2}}{2}$ | B． | 1 | C． | $\sqrt{2}$ | D． | 2$\sqrt{2}$ |
15．f（x）是定义在（0，+∞）上的单调函数，且对?x∈（0，+∞）都有f（f（x）-lnx）=e+1，则方程f（x）-f′（x）=e的实数解所在的区间是（ ）
| A． | （0，$\frac{1}{e}$） | B． | （$\frac{1}{e}$，1） | C． | （1，e） | D． | （e，4） |