题目内容
17.某同学在高三学年的五次阶段性考试中,数学成绩依次为110,114,121,119,126,则这组数据的方差是30.8.
分析 根据平均数与方差的计算公式,计算即可.
解答 解:五次考试的数学成绩分别是110,114,121,119,126,
∴它们的平均数是$\overline{x}$=$\frac{1}{5}$×(110+114+121+119+126)=118,
方差是s2=$\frac{1}{5}$[(110-118)2+(114-118)2+(121-118)2+(119-118)2+(126-118)2]=30.8.
故答案为:30.8.
点评 本题考查平均数与方差的计算问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.已知命题p:△ABC中,若A>B,则cosA>cosB,则下列命题为真命题的是( )
| A. | p的逆命题 | B. | p的否命题 | C. | p的逆否命题 | D. | p的否定 |
12.执行如图所示的程序框图,输出的s=( )


| A. | 5 | B. | 20 | C. | 60 | D. | 120 |
3.已知圆C:x2+y2-4x+m=0与圆${({x-3})^2}+{({y+2\sqrt{2}})^2}=4$外切,点P是圆C一动点,则点P到直线3x-4y+4=0的距离的最大值为( )
| A. | $2\sqrt{2}$ | B. | 3 | C. | 4 | D. | $3\sqrt{2}$ |
20.若存在正实数m,使得关于x的方程x+a(2x+2m-4ex)[1n(x+m)-lnx]=0有两个不同的根,其中e为自然对数的底数,则实数a的取值范围是( )
| A. | (-∞,0) | B. | (0,$\frac{1}{2e}$) | C. | (-∞,0)∪($\frac{1}{2e}$,+∞) | D. | ($\frac{1}{2e}$,+∞) |
1.已知集合A={x|y=lg(x+1)},B={x||x|<2},则A∩B=( )
| A. | (-2,0) | B. | (0,2) | C. | (-1,2) | D. | (-2,-1) |
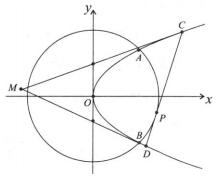 如图,已知抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.
如图,已知抛物线E:y2=2px(p>0)与圆O:x2+y2=8相交于A,B两点,且点A的横坐标为2.过劣弧AB上动点P(x0,y0)作圆O的切线交抛物线E于C,D两点,分别以C,D为切点作抛物线E的切线l1,l2,l1与l2相交于点M.