题目内容
2.已知等差数列{an}中,Sn为其前n项和,S4=π(其中π为圆周率),a4=2a2,现从此数列的前30项中随机选取一个元素,则该元素的余弦值为负数的概率为( )| A. | $\frac{7}{15}$ | B. | $\frac{1}{2}$ | C. | $\frac{8}{15}$ | D. | $\frac{7}{30}$ |
分析 由等差数列{an}前n项和玖通项公式,列出方程组,求出首项和公差,从而得到${a}_{n}=\frac{π}{10}+(n-1)×\frac{π}{10}$=$\frac{nπ}{10}$,进而前30项中,第6至14项和第26项至第30项的余弦值是负数,由此能求出现从此数列的前30项中随机选取一个元素,则该元素的余弦值为负数的概率.
解答 解:∵等差数列{an}中,Sn为其前n项和,S4=π(其中π为圆周率),a4=2a2,
∴$\left\{\begin{array}{l}{{S}_{4}=4{a}_{1}+\frac{4×3}{2}d=π}\\{{a}_{1}+3d=2({a}_{1}+d)}\end{array}\right.$,
解得${a}_{1}=d=\frac{π}{10}$,
∴${a}_{n}=\frac{π}{10}+(n-1)×\frac{π}{10}$=$\frac{nπ}{10}$,
∴前30项中,第6至14项和第26项至第30项的余弦值是负数,
∴现从此数列的前30项中随机选取一个元素,
则该元素的余弦值为负数的概率为p=$\frac{14}{30}$=$\frac{7}{15}$.
故选:A.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
相关题目
12.设(1-i)(x+yi)=2,其中x,y是实数,则x+yi的共轭复数在复平面对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.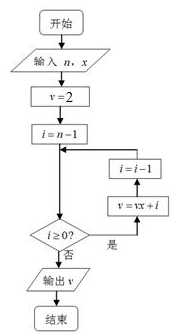 秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )
 秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )| A. | 66 | B. | 33 | C. | 16 | D. | 8 |
14.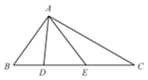 在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
 在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )| A. | 31.2 | B. | 32.4 | C. | 33.6 | D. | 34.8 |
11.在△ABC中,a,b,c分别是角A,B,C的对边,若a=1,b=$\sqrt{3}$,B=60°,则△ABC的面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
12.执行如图所示的程序框图,输出的s=( )


| A. | 5 | B. | 20 | C. | 60 | D. | 120 |
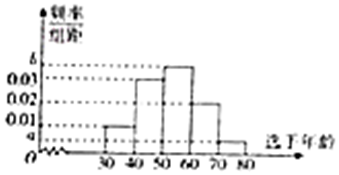 京剧是我国的国粹,是“国家级非物质文化遗产”,为纪念著名京剧表演艺术家、京剧艺术大师梅兰芳先生,某市电视台举办《我爱京剧》的比赛,并随机抽取100位参与《我爱京剧》比赛节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在[30,80]内),样本数据分组区间为[30,40),[40,50),[50,60),[60,70),[70,80],由此得到如图所示的频率分布直方图.
京剧是我国的国粹,是“国家级非物质文化遗产”,为纪念著名京剧表演艺术家、京剧艺术大师梅兰芳先生,某市电视台举办《我爱京剧》的比赛,并随机抽取100位参与《我爱京剧》比赛节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在[30,80]内),样本数据分组区间为[30,40),[40,50),[50,60),[60,70),[70,80],由此得到如图所示的频率分布直方图.