题目内容
3.已知抛物线y2=20x的焦点F恰好为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点,且点F到双曲线的渐近线的距离是4,则双曲线的方程为( )| A. | $\frac{{x}^{2}}{41}$$-\frac{{y}^{2}}{16}$=1 | B. | $\frac{{x}^{2}}{21}$$-\frac{{y}^{2}}{4}$=1 | C. | $\frac{{x}^{2}}{3}$$-\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{9}$$-\frac{{y}^{2}}{16}$=1 |
分析 确定抛物线y2=20x的焦点坐标、双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线的方程,利用抛物线的焦点到双曲线渐近线的距离为4,求出b,a,即可求出双曲线的方程.
解答 解:抛物线y2=20x的焦点坐标为(5,0),双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线的方程为bx+ay=0,
∵抛物线的焦点到双曲线渐近线的距离为4,
∴$\frac{5b}{\sqrt{{b}^{2}+{a}^{2}}}$=4,即b=4,
∵c=5,∴a=3,
∴双曲线方程为:$\frac{{x}^{2}}{9}$$-\frac{{y}^{2}}{16}$=1.
故选:D.
点评 本题考查双曲线的简单性质的应用,抛物线的性质,考查学生的计算能力,比较基础.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
13.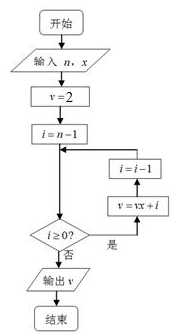 秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )
 秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )
秦九韶是我国南宋时期的数学家,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为4,2,则输出v的值为( )| A. | 66 | B. | 33 | C. | 16 | D. | 8 |
14.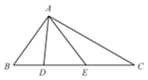 在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
 在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )| A. | 31.2 | B. | 32.4 | C. | 33.6 | D. | 34.8 |
11.在△ABC中,a,b,c分别是角A,B,C的对边,若a=1,b=$\sqrt{3}$,B=60°,则△ABC的面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上的一点到双曲线的左、右焦点的距离之差为4,若抛物线y=ax2上的两点A(x1,y1),B(x2,y2)关于直线y=x+m对称,且x1x2=-$\frac{1}{2}$,则m的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | 2 | D. | 3 |
15.已知集合A={x|y=lg(x-1)},B={x|2${\;}^{{x}^{2}-2x}$<1},则A∩B=( )
| A. | {x|x>1} | B. | {x|x>0} | C. | {x|0<x<2} | D. | {x|1<x<2} |
12.执行如图所示的程序框图,输出的s=( )


| A. | 5 | B. | 20 | C. | 60 | D. | 120 |
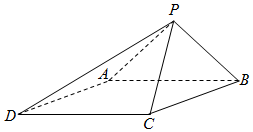 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.