题目内容
20.若α∈($\frac{π}{2}$,π),则3cos2α=cos($\frac{π}{4}$+α),则sin2α的值为( )| A. | $\frac{1}{18}$ | B. | -$\frac{1}{18}$ | C. | $\frac{17}{18}$ | D. | -$\frac{17}{18}$ |
分析 由已知利用二倍角的余弦函数公式,两角和的余弦函数公式化简可得3(cosα+sinα)(cosα-sinα)=$\frac{\sqrt{2}}{2}$(cosα-sinα),由范围α∈($\frac{π}{2}$,π),可得:cosα-sinα≠0,从而可求cosα+sinα=$\frac{\sqrt{2}}{6}$,两边平方,利用同角三角函数基本关系式,二倍角的正弦函数公式即可计算得解.
解答 解:∵3cos2α=cos($\frac{π}{4}$+α),
∴3(cosα+sinα)(cosα-sinα)=$\frac{\sqrt{2}}{2}$(cosα-sinα),
∵α∈($\frac{π}{2}$,π),可得:cosα-sinα≠0,
∴cosα+sinα=$\frac{\sqrt{2}}{6}$,
∴两边平方可得:1+sin2α=$\frac{1}{18}$,解得:sin2α=-$\frac{17}{18}$.
故选:D.
点评 本题主要考查了二倍角的余弦函数公式,两角和的余弦函数公式,同角三角函数基本关系式,二倍角的正弦函数公式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
11.在△ABC中,a,b,c分别是角A,B,C的对边,若a=1,b=$\sqrt{3}$,B=60°,则△ABC的面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
15.已知集合A={x|y=lg(x-1)},B={x|2${\;}^{{x}^{2}-2x}$<1},则A∩B=( )
| A. | {x|x>1} | B. | {x|x>0} | C. | {x|0<x<2} | D. | {x|1<x<2} |
5.已知命题p:△ABC中,若A>B,则cosA>cosB,则下列命题为真命题的是( )
| A. | p的逆命题 | B. | p的否命题 | C. | p的逆否命题 | D. | p的否定 |
12.执行如图所示的程序框图,输出的s=( )


| A. | 5 | B. | 20 | C. | 60 | D. | 120 |
3.已知圆C:x2+y2-4x+m=0与圆${({x-3})^2}+{({y+2\sqrt{2}})^2}=4$外切,点P是圆C一动点,则点P到直线3x-4y+4=0的距离的最大值为( )
| A. | $2\sqrt{2}$ | B. | 3 | C. | 4 | D. | $3\sqrt{2}$ |
4.已知抛物线C:y2=2px(0<p<4)的焦点为F,点P为C上一动点,A(4,0),B(p,$\sqrt{2}$p),且|PA|的最小值为$\sqrt{15}$,则|BF|等于( )
| A. | 4 | B. | $\frac{7}{2}$ | C. | 5 | D. | $\frac{9}{2}$ |
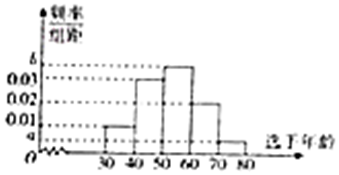 京剧是我国的国粹,是“国家级非物质文化遗产”,为纪念著名京剧表演艺术家、京剧艺术大师梅兰芳先生,某市电视台举办《我爱京剧》的比赛,并随机抽取100位参与《我爱京剧》比赛节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在[30,80]内),样本数据分组区间为[30,40),[40,50),[50,60),[60,70),[70,80],由此得到如图所示的频率分布直方图.
京剧是我国的国粹,是“国家级非物质文化遗产”,为纪念著名京剧表演艺术家、京剧艺术大师梅兰芳先生,某市电视台举办《我爱京剧》的比赛,并随机抽取100位参与《我爱京剧》比赛节目的票友的年龄作为样本进行分析研究(全部票友的年龄都在[30,80]内),样本数据分组区间为[30,40),[40,50),[50,60),[60,70),[70,80],由此得到如图所示的频率分布直方图.