题目内容
4.在直角坐标系xOy中,以坐标原点为极点,x轴的非负半轴为极轴建立极坐标系,圆C的极坐标方程为ρ=4cosθ.(1)求出圆C的直角坐标方程;
(2)已知圆C与x轴相交于A,B两点,直线l:y=2x关于点M(0,m)(m≠0)对称的直线为l'.若直线l'上存在点P使得∠APB=90°,求实数m的最大值.
分析 (1)由ρ=4cosθ得ρ2=4ρcosθ,即可求出圆C的直角坐标方程;
(2)l:y=2x关于点M(0,m)的对称直线l'的方程为y=2x+2m,而AB为圆C的直径,故直线l'上存在点P使得∠APB=90°的充要条件是直线l'与圆C有公共点,即可求实数m的最大值.
解答 解:(1)由ρ=4cosθ得ρ2=4ρcosθ,即x2+y2-4x=0,即圆C的标准方程为(x-2)2+y2=4.
(2)l:y=2x关于点M(0,m)的对称直线l'的方程为y=2x+2m,而AB为圆C的直径,故直线l'上存在点P使得∠APB=90°的充要条件是直线l'与圆C有公共点,故$\frac{{|{4+2m}|}}{{\sqrt{5}}}≤2$,于是,实数m的最大值为$\sqrt{5}-2$.
点评 本题考查极坐标方程转化为直角坐标方程,考查直线与圆的位置关系的运用,考查学生转化问题的能力,属于中档题.

练习册系列答案
相关题目
14.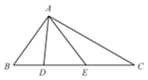 在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
 在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )| A. | 31.2 | B. | 32.4 | C. | 33.6 | D. | 34.8 |
15.已知集合A={x|y=lg(x-1)},B={x|2${\;}^{{x}^{2}-2x}$<1},则A∩B=( )
| A. | {x|x>1} | B. | {x|x>0} | C. | {x|0<x<2} | D. | {x|1<x<2} |
12.执行如图所示的程序框图,输出的s=( )


| A. | 5 | B. | 20 | C. | 60 | D. | 120 |
3.已知圆C:x2+y2-4x+m=0与圆${({x-3})^2}+{({y+2\sqrt{2}})^2}=4$外切,点P是圆C一动点,则点P到直线3x-4y+4=0的距离的最大值为( )
| A. | $2\sqrt{2}$ | B. | 3 | C. | 4 | D. | $3\sqrt{2}$ |
10.已知函数f(x)=2x的值域为A,g(x)=lnx的定义域为B,则( )
| A. | A∩B=(0,1) | B. | A∪B=R | C. | B?A | D. | A=B |
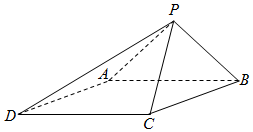 如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.
如图,已知四棱锥P-ABCD的底面为菱形,∠BCD=120°,AB=PC=2,AP=BP=$\sqrt{2}$.