题目内容
设等比数列{an}满足a1+a2=1，a3+a4=3，则a5+a6=（ ）
| A、6 | B、9或-9 |
| C、6或-6 | D、9 |
考点：等比数列的性质
专题：等差数列与等比数列
分析：由题意可得q2，而a5+a6=（a3+a4）q2，代值计算可得．
解答：
解：设等比数列{an}的公比为q，
则q2=
=3，
∴a5+a6=（a3+a4）q2=3×3=9，
故选：D
则q2=
| a3+a4 |
| a1+a2 |
∴a5+a6=（a3+a4）q2=3×3=9，
故选：D
点评：本题考查等比数列的性质，属基础题．
练习册系列答案
相关题目
已知z1、z2∈C，|z1+z2|=2
，|z1|=
，|z2|=
，则|z1-z2|等于（ ）
| 2 |
| 3 |
| 2 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
下列函数中，在（0，2）内有零点且单调递增的是（ ）
| A、y=2x-2 | ||
B、y=log
| ||
| C、y=|x|-3 | ||
| D、y=-x3 |
西华三高学生会随机对高二文科班的50名学生进行了上课是否睡觉的调查，数据如下表：
根据表中数据得到k=
≈5.059，则认为带手机与上课睡觉有关系的把握大约为（ ）
| 上课常睡觉 | 上课不睡觉 | 总数 | |
| 带手机 | 18 | 9 | 27 |
| 没带手机 | 8 | 15 | 23 |
| 总数 | 26 | 24 | 50 |
| 50×(18×15-8×9)2 |
| 27×23×24×26 |
| A、90% | B、95% |
| C、97.5% | D、无充分根据 |
若实数a，b，c，d满足a＞b，c＞d，则下列不等式成立的是（ ）
| A、a-c＞b-d | ||||
| B、a+c＞b+d | ||||
| C、ac＞bd | ||||
D、
|
已知i为虚数单位，则i（1+i）2=（ ）
| A、2i | B、-2i | C、2 | D、-2 |
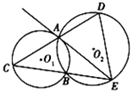已知⊙O1和⊙O2相交于A，B两点，过A点作⊙O1的切线交⊙O2于点E，连接EB并延长交⊙O1于点C，直线CA交⊙O2于点D．