题目内容
西华三高学生会随机对高二文科班的50名学生进行了上课是否睡觉的调查，数据如下表：
根据表中数据得到k=
≈5.059，则认为带手机与上课睡觉有关系的把握大约为（ ）
| 上课常睡觉 | 上课不睡觉 | 总数 | |
| 带手机 | 18 | 9 | 27 |
| 没带手机 | 8 | 15 | 23 |
| 总数 | 26 | 24 | 50 |
| 50×(18×15-8×9)2 |
| 27×23×24×26 |
| A、90% | B、95% |
| C、97.5% | D、无充分根据 |
考点：独立性检验的基本思想
专题：计算题,概率与统计
分析：根据条件中所给的计算出的观测值的数据，把观测值同临界值进行比较，得到认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为1-0.025=97.5%．
解答：
解：∵根据表中数据得到k=
≈5.059，
因为p（K2≥5.024）=0.025，
∴认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为1-0.025=97.5%
故选：C．
| 50×(18×15-8×9)2 |
| 27×23×24×26 |
因为p（K2≥5.024）=0.025，
∴认为喜欢玩电脑游戏与认为作业量的多少有关系的把握大约为1-0.025=97.5%
故选：C．
点评：本题考查独立性检验的应用，本题解题的关键是理解临界值对应的概率的应用，能够正确的说出概率的意义．
练习册系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
方程x2+y2+ax-2ay+a2+3a=0表示的图形是半径为r（a＞0）的圆，则该圆 圆心在（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
集合A={x|x2-2x＜0}，B={y|y=2x，x＞0}，R是实数集，则A∩B=（ ）
| A、（0，+∞） |
| B、（-∞，0）∪（2，+∞） |
| C、（0，1） |
| D、（1，2） |
若函数f（x）在R上可导，且满足f（x）＜xf′（x），则（ ）
| A、2f（1）＜f（2） |
| B、2f（1）＞f（2） |
| C、2f（1）=f（2） |
| D、f（1）=f（2） |
若函数f（x）=logax的图象与直线y=
x相切，则a的值为（ ）
| 1 |
| 3 |
A、e
| ||
B、e
| ||
C、
| ||
D、e
|
已知m，n是不同的两条直线，α，β是不同的两个平面，则下列命题中不正确的是（ ）
| A、若m∥n，m⊥α，则n⊥α |
| B、若m∥α，α∩β=n，则m∥n |
| C、若m⊥α，m?β，则α⊥β |
| D、若m⊥α，m⊥β，则α∥β |
设等比数列{an}满足a1+a2=1，a3+a4=3，则a5+a6=（ ）
| A、6 | B、9或-9 |
| C、6或-6 | D、9 |
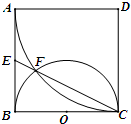如图，正方形ABCD边长为2，以D为圆心、DA为半径的圆弧与以BC为直径的半圆O交于点F，连结CF并延长交AB于点E．
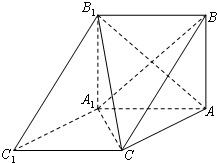如图，三棱柱ABC-A1B1C1中，BA⊥平面AA1C1C，AB=2