题目内容
已知等腰三角形△ABC三边为a,b,c三边所对角为A,B,C,满足 bcosC+ccosB=
R.R为三角形ABC的外接圆半径.
(1)求角A.
(2)若a=1,求△ABC的周长.
| 3 |
(1)求角A.
(2)若a=1,求△ABC的周长.
考点:余弦定理,正弦定理
专题:解三角形
分析:(1)等腰三角形△ABC中,由条件正弦定理】诱导公式求得sinA=
,可得A的值.
(2)由a=1,可得当A=
时,△ABC为等边三角形,求得此时三角形的周长为3;当A=
时,利用正弦定理求得b、c的值,可得三角形的周长,综合可得结论.
| ||
| 2 |
(2)由a=1,可得当A=
| π |
| 3 |
| 2π |
| 3 |
解答:
解:(1)等腰三角形△ABC中,∵bcosC+ccosB=
R,则由正弦定理可得sinBcosC+cosBsinC=
,
即sin(B+C)=
=sinA,∴sinA=
,∴A=
,或A=
.
(2)∵a=1,当A=
时,△ABC为等边三角形,此时三角形的周长为3;
当A=
时,B=C=
,由a=1利用正弦定理可得
=
,即
=
,b=
=c,
此时,三角形的周长为1+
.
综上可得,三角形的周长为3 或1+
.
| 3 |
| ||
| 2 |
即sin(B+C)=
| ||
| 2 |
| ||
| 2 |
| π |
| 3 |
| 2π |
| 3 |
(2)∵a=1,当A=
| π |
| 3 |
当A=
| 2π |
| 3 |
| π |
| 6 |
| b | ||
sin
|
| a |
| sinA |
| b | ||
|
| 1 | ||||
|
| ||
| 3 |
此时,三角形的周长为1+
2
| ||
| 3 |
综上可得,三角形的周长为3 或1+
2
| ||
| 3 |
点评:本题主要考查正弦定理、诱导公式的应用,属于基础题.

练习册系列答案
相关题目
设α是第二象限角,p(x,4)为其终边上的一点,且cosα=
x,则sinα=( )
| 1 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
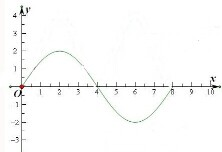 已知函数f(x)=Asinωx(A>0,ω<0)的部分图象如图所示,则函数f(x)是( )
已知函数f(x)=Asinωx(A>0,ω<0)的部分图象如图所示,则函数f(x)是( )| A、周期为8的偶函数 |
| B、周期为8的奇函数 |
| C、周期为8π的偶函数 |
| D、周期为8π的奇函数 |