题目内容
若等边△ABC的边长为2
，平面内一点M满足
=
+
，则
•
= ．
| 3 |
| CM |
| 1 |
| 6 |
| CB |
| 2 |
| 3 |
| CA |
| MA |
| MB |
考点：平面向量数量积的运算
专题：平面向量及应用
分析：由等边△ABC的边长为2
，可得
•
=6．再利用向量的三角形法则可得
=
+
，
=
+
，代入
•
=(
+
)•(
+
)=(-
-
+
)•(-
-
+
)即可得出．
| 3 |
| CA |
| CB |
| MA |
| MC |
| CA |
| MB |
| MC |
| CB |
| MA |
| MB |
| MC |
| CA |
| MC |
| CB |
| 1 |
| 6 |
| CB |
| 2 |
| 3 |
| CA |
| CA |
| 1 |
| 6 |
| CB |
| 2 |
| 3 |
| CA |
| CB |
解答：
解：如图所示，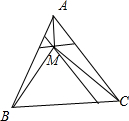
由等边△ABC的边长为2
，
∴
•
=|
| |
|cos60°=2
×2
×
=6．
∵
=
+
，
=
+
，
∴
•
=(
+
)•(
+
)
=(-
-
+
)•(-
-
+
)
=(
-
)•(
-
)
=-
2-
2+
•
=-
×(2
)2-
×(2
)2+
×6
=-2．
故答案为：-2．
由等边△ABC的边长为2| 3 |
∴
| CA |
| CB |
| CA |
| CB |
| 3 |
| 3 |
| 1 |
| 2 |
∵
| MA |
| MC |
| CA |
| MB |
| MC |
| CB |
∴
| MA |
| MB |
| MC |
| CA |
| MC |
| CB |
=(-
| 1 |
| 6 |
| CB |
| 2 |
| 3 |
| CA |
| CA |
| 1 |
| 6 |
| CB |
| 2 |
| 3 |
| CA |
| CB |
=(
| 1 |
| 3 |
| CA |
| 1 |
| 6 |
| CB |
| 5 |
| 6 |
| CB |
| 2 |
| 3 |
| CA |
=-
| 2 |
| 9 |
| CA |
| 5 |
| 36 |
| CB |
| 7 |
| 18 |
| CA |
| CB |
=-
| 2 |
| 9 |
| 3 |
| 5 |
| 36 |
| 3 |
| 7 |
| 18 |
=-2．
故答案为：-2．
点评：本题考查了向量的三角形法则、数量积运算法则，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
如图，矩形ABCD所在的半平面和直角梯形CDEF所在的半平面成60°的二面角，DE∥CF，CD⊥DE，AD=2，EF=3