题目内容
已知三个正数a,b,c满足a2,b2,c2成等差数列,求证
,
,
也成等差数列.
| 1 |
| a+b |
| 1 |
| a+c |
| 1 |
| b+c |
考点:等差关系的确定
专题:等差数列与等比数列
分析:根据等差数列的定义进行证明即可.
解答:
解:∵三个正数a,b,c满足a2,b2,c2成等差数列,
∴a2+c2=2b2,
∵
+
=
,
∴要使
=
成立,
则等价为2ab+2b2+2bc+2ac=a2+2ab+ac+ac+2bc+c2,
化简得2b2=a2+c2,此式成立,
∴结论成立.
综上证
,
,
也成等差数列.
∴a2+c2=2b2,
∵
| 1 |
| a+b |
| 1 |
| b+c |
| a+2b+c |
| (b+c)(a+b) |
∴要使
| a+2b+c |
| (b+c)(a+b) |
| 2 |
| a+c |
则等价为2ab+2b2+2bc+2ac=a2+2ab+ac+ac+2bc+c2,
化简得2b2=a2+c2,此式成立,
∴结论成立.
综上证
| 1 |
| a+b |
| 1 |
| a+c |
| 1 |
| b+c |
点评:本题主要考查等差数列的定义和判断,考查学生的运算和推理能力.

练习册系列答案
相关题目
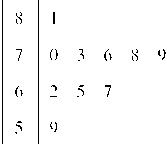 已知某单位有50名职工,现要从中抽取10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组进行系统抽样.
已知某单位有50名职工,现要从中抽取10名职工,将全体职工随机按1~50编号,并按编号顺序平均分成10组进行系统抽样.