题目内容
14.函数y=2016x-sinx的图象大致是( )| A. | 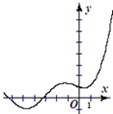 | B. | 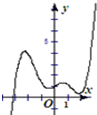 | C. | 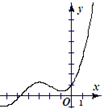 | D. | 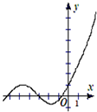 |
分析 求导y′=2016xln2016-cosx,从而确定导数的正负及函数的单调性,从而利用排除法求得.
解答 解:∵y=2016x-sinx,
∴y′=2016xln2016-cosx,
当x≥0时,y′>0;
故函数y=2016x-sinx在[0,+∞)上是增函数,
故排除A,B;
y′=2016xln2016-cosx在[-1,0]上单调递增,
且在[-1,0]上先负后正,
故y=2016x-sinx在[-1,0]上有极小值,
而在[-1,0]上,y=2016x-sinx>0恒成立;
故排除D;
故选C.
点评 本题考查了导数的综合应用及数形结合的思想方法应用,同时考查了函数的性质应用.

练习册系列答案
相关题目
5.下列说法中,正确的是( )
| A. | 命题“若am2<bm2,则a<b”的逆命题是真命题 | |
| B. | 在△ABC中,若acosA=bcosB,则△ABC为等腰直角三角形 | |
| C. | 函数y=ax2+bx+c为偶函数的充要条件是b=0 | |
| D. | b=$\sqrt{ac}$是a,b,c成等比的必要不充分条件 |
2.已知直线l1:3x+4y-3=0,直线l2:6x+8y-1=0平行,则它们之间的距离为( )
| A. | 2 | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | 1 |
9.若等比数列{a${\;}_{{n}_{\;}}$}的公比为q(q≠0),则关于x、y的二元一次方程组$\left\{\begin{array}{l}{{a}_{1}x+{a}_{3}y=3}\\{{a}_{2}x+{a}_{4}y=-2}\end{array}\right.$的解的情况的下列说法中正确的是( )
| A. | 对任意q∈R(q≠0),方程组都有唯一解 | |
| B. | 对任意q∈R(q≠0),方程组都无解 | |
| C. | 当且仅当q=-$\frac{2}{3}$时,方程组有无穷多解 | |
| D. | 当且仅当q=-$\frac{2}{3}$时,方程组无解 |