题目内容
2.已知直线l1:3x+4y-3=0,直线l2:6x+8y-1=0平行,则它们之间的距离为( )| A. | 2 | B. | $\frac{1}{5}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 利用两条平行线之间的距离公式即可得出.
解答 解:直线l2:6x+8y-1=0化为:3x+4y-$\frac{1}{2}$=0.
∴两条平行线之间的距离d=$\frac{|-3-(-\frac{1}{2})|}{\sqrt{{3}^{2}+{4}^{2}}}$=$\frac{1}{2}$.
故选:C.
点评 本题考查了两条平行线之间的距离公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
10.已知等差数列{an},{bn}的公差分别是p,q(pq≠0),则数列{an+bn}( )
| A. | 是公差为p的等差数列 | B. | 是公差为q的等差数列 | ||
| C. | 是公差为p+q的等差数列 | D. | 不是等差数列 |
17.若点P(x,y)为不等式组$\left\{\begin{array}{l}2x-y-2≥0\\ x+2y-1≥0\\ 3x+y-8≤0\end{array}\right.$所表示区域内任一点,则x2+y2+1的最小值为( )
| A. | $-\frac{1}{3}$ | B. | 1 | C. | 2 | D. | $-\frac{1}{2}$ |
7.f(x)=sin(x-α),f(x)在〔0,$\frac{π}{3}$〕上的定积分等于0,则tanα=( )
| A. | $\sqrt{3}$ | B. | -$\sqrt{3}$ | C. | $\frac{1}{{\sqrt{3}}}$ | D. | -$\frac{1}{{\sqrt{3}}}$ |
14.函数y=2016x-sinx的图象大致是( )
| A. | 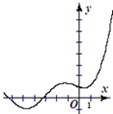 | B. | 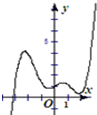 | C. | 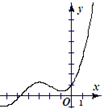 | D. | 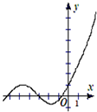 |
12.函数f(x)=sinωx(ω>0)在区间(-$\frac{2π}{3}$,$\frac{π}{3}$)上有且只有2个极值点,则ω的取值范围是( )
| A. | [$\frac{3}{2}$,$\frac{9}{4}$] | B. | ($\frac{3}{2}$,$\frac{9}{4}$) | C. | ($\frac{3}{2}$,$\frac{9}{4}$] | D. | [$\frac{3}{2}$,$\frac{9}{4}$) |