题目内容
5.下列说法中,正确的是( )| A. | 命题“若am2<bm2,则a<b”的逆命题是真命题 | |
| B. | 在△ABC中,若acosA=bcosB,则△ABC为等腰直角三角形 | |
| C. | 函数y=ax2+bx+c为偶函数的充要条件是b=0 | |
| D. | b=$\sqrt{ac}$是a,b,c成等比的必要不充分条件 |
分析 A.原命题的逆命题为“若a<b,则am2<bm2”,m=0时不成立;
B.△ABC中,若acosA=bcosB,利用正弦定理可得:sinAcosA=sinBcosB,可得sin2A=sin2B,可得2A=2B,或2A+2B=π,即可判断出结论.
C.y=ax2+bx+c为偶函数?f(-x)=f(x)?bx=0,即可判断出真假;
D.b=$\sqrt{ac}$是a,b,c成等比的既不充分也不必要条件.
解答 解:A.命题“若am2<bm2,则a<b”的逆命题为“若a<b,则am2<bm2”,m=0时不成立,因此是假命题;
B.△ABC中,若acosA=bcosB,则sinAcosA=sinBcosB,可得sin2A=sin2B,A,B∈(0,π),
∴2A=2B,或2A+2B=π,可得A=B,A+B=$\frac{π}{2}$,
∴△ABC为等腰或直角三角形,因此不正确;
C.y=ax2+bx+c为偶函数?f(-x)=f(x)?bx=0?b=0,正确;
D.b=$\sqrt{ac}$是a,b,c成等比的既不充分也不必要条件,因此不正确.
故选:C.
点评 本题考查了简易逻辑的判定方法、正弦定理的应用、函数的奇偶性、等比数列,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
10.已知等差数列{an},{bn}的公差分别是p,q(pq≠0),则数列{an+bn}( )
| A. | 是公差为p的等差数列 | B. | 是公差为q的等差数列 | ||
| C. | 是公差为p+q的等差数列 | D. | 不是等差数列 |
17.若点P(x,y)为不等式组$\left\{\begin{array}{l}2x-y-2≥0\\ x+2y-1≥0\\ 3x+y-8≤0\end{array}\right.$所表示区域内任一点,则x2+y2+1的最小值为( )
| A. | $-\frac{1}{3}$ | B. | 1 | C. | 2 | D. | $-\frac{1}{2}$ |
14.函数y=2016x-sinx的图象大致是( )
| A. | 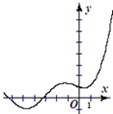 | B. | 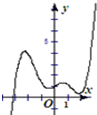 | C. | 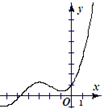 | D. | 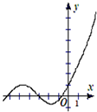 |
15.已知在等比数列{an}中,Sn是{an}的前n项和,a1+a3=10,S4=15,则该数列的公比等于( )
| A. | 2 | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
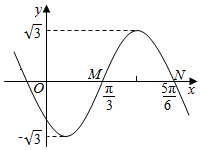 如图为函数y=f(x)=Asin(wx+φ)(A>3,w>0,|φ|<π)图象的一部分.
如图为函数y=f(x)=Asin(wx+φ)(A>3,w>0,|φ|<π)图象的一部分.