题目内容
4.已知等差数列{an}的首项为21,公差为-2,则当n=11时,该数列的前n项和Sn取得最大值.分析 由等差数列的通项公式先求出an,再由an≥0,能求出该数列的前n项和Sn取得最大值时n的值.
解答 解:∵等差数列{an}的首项为21,公差为-2,
∴an=21+(n-1)×(-2)=23-2n,
由an=23-2n≥0,得n≤11$\frac{1}{2}$.
∴当n=11时,该数列的前n项和Sn取得最大值.
故答案为:11.
点评 本题考查数列的最大值的求法,是基础题,解题时要认真审题,注意等差数列的性质的合理运用.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
19.在同一坐标系中,函数y=3-x与y=3x的图象之间的关系是( )
| A. | 关于原点对称 | B. | 关于直线y=x对称 | C. | 关于x轴对称 | D. | 关于y轴对称 |
14.函数y=2016x-sinx的图象大致是( )
| A. | 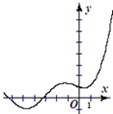 | B. | 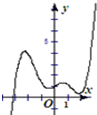 | C. | 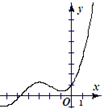 | D. | 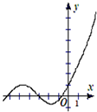 |
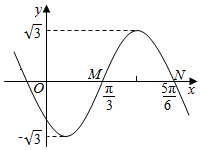 如图为函数y=f(x)=Asin(wx+φ)(A>3,w>0,|φ|<π)图象的一部分.
如图为函数y=f(x)=Asin(wx+φ)(A>3,w>0,|φ|<π)图象的一部分. 设函数f(x)=|log2(x+2)|-1.
设函数f(x)=|log2(x+2)|-1.